Sortiranje predstavlja jednu od najčešće primenjivanih operacija u svetu programiranja. Efektivnost sortiranja zavisi od izbora odgovarajućeg algoritma, stoga je važno razmotriti različite pristupe.
U ovom tekstu istražićemo različite metode sortiranja.
Detaljno ćemo analizirati različite algoritme za sortiranje, uzimajući u obzir svaki korak njihove implementacije. Implementacija će biti predstavljena u Pythonu, ali lako se može adaptirati na bilo koji drugi programski jezik, pošto je suština u logici algoritma, a ne sintaksi.
Ovaj vodič će obuhvatiti različite algoritme, od manje efikasnih do onih sa boljim performansama. Pratite pažljivo i primenite stečeno znanje.
Krenimo sa istraživanjem algoritama za sortiranje.
Insertion Sort (Sortiranje umetanjem)
Sortiranje umetanjem spada u jednostavnije metode sortiranja, laku za implementaciju, ali može zahtevati više vremena za sortiranje većih nizova. Stoga, nije najprikladnija za obimne skupove podataka.
Ovaj algoritam deli niz na sortirani i nesortirani deo.
U početnoj fazi, sortirani deo se sastoji od prvog elementa. Zatim, uzimamo element iz nesortiranog dela i umećemo ga na pravo mesto u sortiranom delu.
Pogledajmo vizuelnu demonstraciju sortiranja umetanjem, korak po korak, na konkretnom primeru.
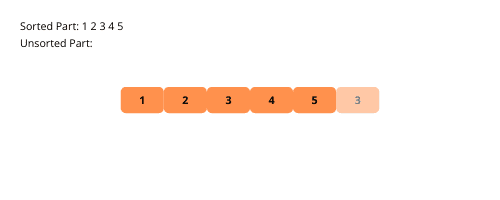
Sada, razmotrimo korake potrebne za implementaciju sortiranja umetanjem:
- Inicijalizujte niz sa proizvoljnim podacima (celim brojevima).
- Iterirajte kroz niz, počevši od drugog elementa.
- Zabeležite trenutnu poziciju i element u dve promenljive.
- Kreirajte petlju koja se izvršava dok se ne dođe do prvog elementa niza, ili dok se ne pronađe element manji od trenutnog elementa.
- Ažurirajte trenutni element sa prethodnim elementom.
- Smanjite trenutnu poziciju.
- Kada se petlja završi, postavi trenutni element na odgovarajuću poziciju.
Vremenska složenost algoritma sortiranja umetanjem iznosi O(n^2), dok je prostorna složenost O(1).
Niz je sortiran. Sledi primer implementacije u Pythonu. U slučaju da nemate Python, možete koristiti onlajn Python kompajler.
def insertion_sort(arr, n): for i in range(1, n): ## current position and element current_position = i current_element = arr[i] ## iteratin until ### it reaches the first element or ### the current element is smaller than the previous element while current_position > 0 and current_element < arr[current_position - 1]: ## updating the current element with previous element arr[current_position] = arr[current_position - 1] ## moving to the previous position current_position -= 1 ## updating the current position element arr[current_position] = current_element if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] insertion_sort(arr, 9) ## printing the array print(str(arr))
Selection Sort (Sortiranje selekcijom)
Sortiranje selekcijom je slično sortiranju umetanjem, sa malom razlikom. Ovaj algoritam takođe deli niz na sortirane i nesortirane delove. U svakoj iteraciji, bira najmanji element iz nesortiranog dela i postavlja ga na kraj sortiranog dela.
Pogledajmo vizuelne ilustracije sortiranja selekcijom radi boljeg razumevanja.
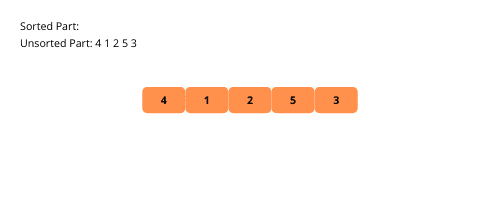
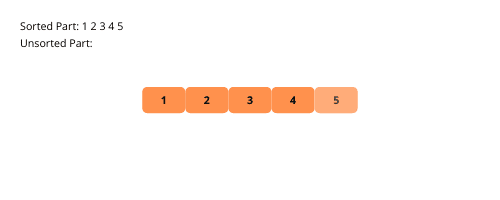
Sledi lista koraka za implementaciju sortiranja selekcijom:
- Inicijalizujte niz sa proizvoljnim podacima (celim brojevima).
- Iterirajte kroz niz.
- Zadržite indeks minimalnog elementa.
- Kreirajte petlju koja se ponavlja od trenutnog do poslednjeg elementa.
- Proverite da li je trenutni element manji od minimalnog elementa.
- Ako jeste, zamenite indekse.
- Nakon petlje, imamo indeks minimalnog elementa. Zamenite trenutni element sa minimalnim elementom koristeći indekse.
Vremenska složenost sortiranja selekcijom iznosi O(n^2), a prostorna složenost O(1).
Pokušajte da sami implementirate algoritam, pošto je sličan sortiranju umetanjem. Kod je dat u nastavku:
def selection_sort(arr, n): for i in range(n): ## to store the index of the minimum element min_element_index = i for j in range(i + 1, n): ## checking and replacing the minimum element index if arr[j] < arr[min_element_index]: min_element_index = j ## swaping the current element with minimum element arr[i], arr[min_element_index] = arr[min_element_index], arr[i] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] selection_sort(arr, 9) ## printing the array print(str(arr))
Bubble Sort (Sortiranje mehurićem)
Sortiranje mehurićem je jednostavan algoritam koji upoređuje i menja susedne elemente u svakoj iteraciji sve dok se niz ne sortira.
Algoritam prolazi kroz niz i premešta trenutni element na sledeću poziciju sve dok ne postane manji od sledećeg elementa.
Ilustracije mogu pomoći da se bolje razume algoritam. Pogledajmo ih.
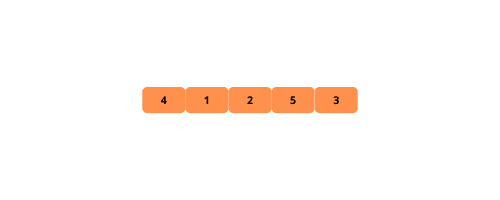
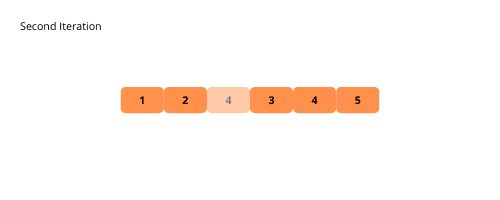
Koraci za implementaciju sortiranja mehurićem su sledeći:
Vremenska složenost sortiranja mehurićem je O(n^2), a prostorna složenost O(1).
Do sada ste verovatno stekli dovoljno znanja da sami implementirate ovaj algoritam. Pogledajte kod:
def bubble_sort(arr, n): for i in range(n): ## iterating from 0 to n-i-1 as last i elements are already sorted for j in range(n - i - 1): ## checking the next element if arr[j] > arr[j + 1]: ## swapping the adjucent elements arr[j], arr[j + 1] = arr[j + 1], arr[j] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] bubble_sort(arr, 9) ## printing the array print(str(arr))
Merge Sort (Sortiranje spajanjem)
Sortiranje spajanjem je rekurzivni algoritam koji deli niz na dva dela i sortira ih zasebno. Nakon toga, spaja sortirane delove u jedan sortirani niz. Ovo je efikasniji algoritam od prethodnih.
Pošto je rekurzivan, ovaj algoritam deli niz sve dok ne dođe do najjednostavnijeg oblika (niz sa jednim elementom).
Pogledajmo ilustraciju:
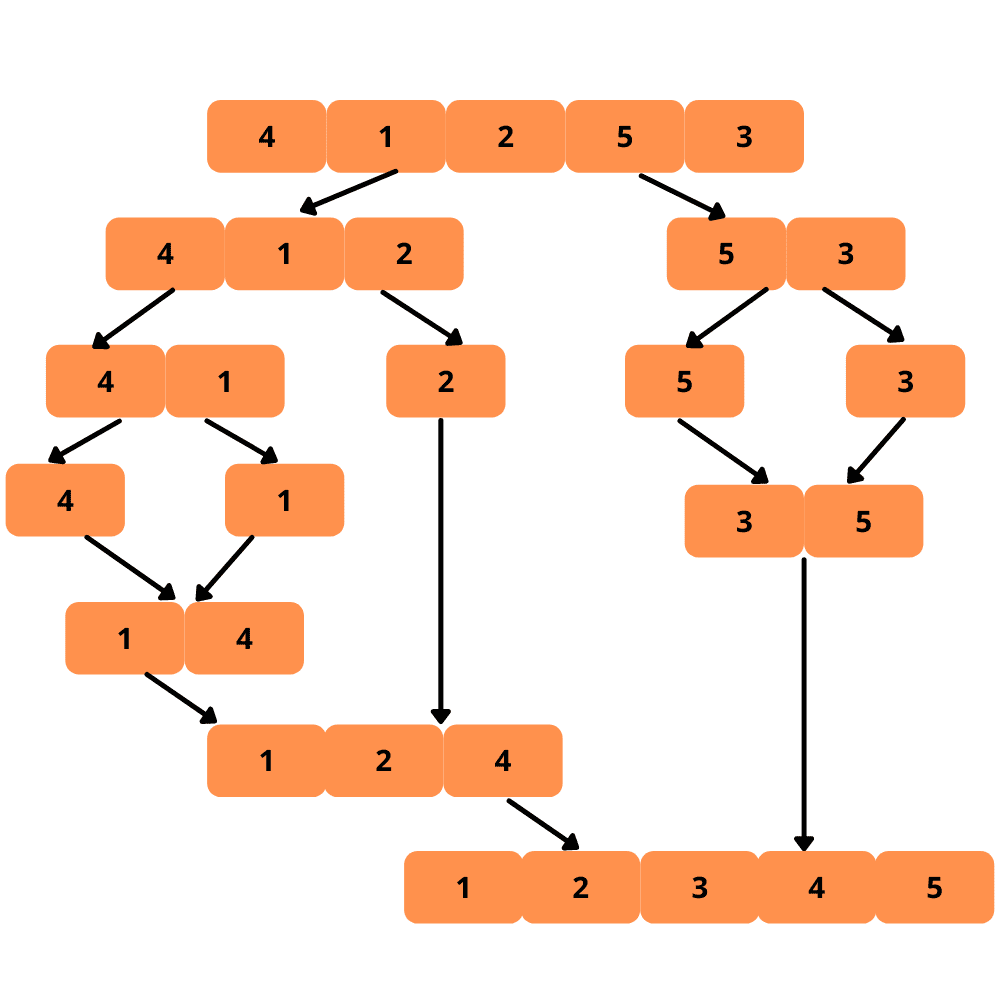
Koraci za implementaciju sortiranja spajanjem:
- Inicijalizujte niz sa proizvoljnim podacima (celim brojevima).
- Napravite funkciju `merge` koja će spajati podnizove u jedan sortirani niz. Funkcija prima niz kao argument, kao i levi, srednji i desni indeks.
- Izračunajte dužine levog i desnog podniza koristeći indekse.
- Kopirajte elemente iz niza u odgovarajuće leve i desne nizove.
- Iterirajte kroz dva podniza.
- Uporedite elemente iz podnizova.
- Zamenite element niza manjim elementom iz dva podniza.
- Proverite da li ima preostalih elemenata u podnizovima.
- Dodajte ih u niz.
- Napravite funkciju `merge_sort` sa nizom parametara, levim i desnim indeksom.
- Ako je levi indeks veći ili jednak desnom, vratite se.
- Pronađite srednju tačku niza.
- Rekurzivno pozovite `merge_sort` koristeći levi, desni i srednji indeks.
- Nakon rekurzivnih poziva, spojite niz pomoću funkcije `merge`.
Vremenska složenost sortiranja spajanjem je O(n log n), a prostorna složenost je O(n).
Implementacija algoritma je sledeća:
def merge(arr, left_index, mid_index, right_index): ## left and right arrays left_array = arr[left_index:mid_index+1] right_array = arr[mid_index+1:right_index+1] ## getting the left and right array lengths left_array_length = mid_index - left_index + 1 right_array_length = right_index - mid_index ## indexes for merging two arrays i = j = 0 ## index for array elements replacement k = left_index ## iterating over the two sub-arrays while i < left_array_length and j < right_array_length: ## comapring the elements from left and right arrays if left_array[i] < right_array[j]: arr[k] = left_array[i] i += 1 else: arr[k] = right_array[j] j += 1 k += 1 ## adding remaining elements from the left and right arrays while i < left_array_length: arr[k] = left_array[i] i += 1 k += 1 while j < right_array_length: j += 1 k += 1 def merge_sort(arr, left_index, right_index): ## base case for recursive function if left_index >= right_index: return ## finding the middle index mid_index = (left_index + right_index) // 2 ## recursive calls merge_sort(arr, left_index, mid_index) merge_sort(arr, mid_index + 1, right_index) ## merging the two sub-arrays merge(arr, left_index, mid_index, right_index) if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] merge_sort(arr, 0, 8) ## printing the array print(str(arr))
Zaključak
Postoji mnogo drugih algoritama za sortiranje, ali ovi su neki od najčešće korišćenih. Nadamo se da ste uživali u učenju o sortiranju.
Sledeće, naučite o algoritmima za pretraživanje.
Srećno sa kodiranjem! 🙂 👨💻