Od prvobitne zamisli o kvantnom računaru tokom 1980-ih do današnjeg dana, oblast kvantnog računarstva je doživela značajan rast, posebno u poslednjih deset godina. Brojne kompanije širom sveta aktivno rade na razvoju kvantnih računara.
Razumevanje kvantnog računarstva može predstavljati izazov za većinu ljudi, a mnogi izvori informacija ne pružaju dovoljno detaljna objašnjenja ključnih aspekata.
Ovaj tekst ima za cilj da razjasni tu temu, a nakon čitanja, steći ćete sveobuhvatno razumevanje suštine kvantnog računarstva, različitih vrsta, načina funkcionisanja, algoritama, modela, pristupa, izazova i potencijalnih primena.
Šta su kvantni računari?
Kvantni računari pristupaju rešavanju problema na način koji se razlikuje od tradicionalnih, odnosno klasičnih računara, kako ćemo ih zvati u nastavku teksta.
Kvantni računari imaju određene prednosti u odnosu na obične računare kada je reč o rešavanju specifičnih vrsta problema. Ovo proizilazi iz njihove sposobnosti da budu u velikom broju stanja istovremeno, dok klasični računari mogu biti samo u jednom stanju u datom trenutku.
Izvor slike: IBM
Da biste razumeli ovu razliku i princip rada kvantnih računara, neophodno je da razumete tri osnovna koncepta: superpoziciju, preplitanje i interferenciju.
Osnovna jedinica informacija u običnom računaru je bit, dok je kod kvantnih računara to kvantni bit, skraćeno kubit. Oni funkcionišu na suštinski različite načine.
Klasičan bit je poput prekidača koji može biti ili u stanju 0 ili u stanju 1. Ovo je verovatno već poznato kao binarna informacija. Prilikom merenja, dobijamo samo trenutno stanje, ali situacija je drugačija kod kubita. Kubit je znatno kompleksniji.
Superpozicija
Radi lakše vizualizacije, zamislite kubit kao strelicu koja pokazuje u trodimenzionalnom prostoru. Ako pokazuje nagore, kubit je u stanju 1, a ako pokazuje nadole, onda je u stanju 0, baš kao i klasičan bit. Međutim, kubit ima i mogućnost da bude u takozvanom stanju superpozicije, kada strelica pokazuje u bilo kom drugom pravcu.
Ovo stanje superpozicije predstavlja kombinaciju stanja 0 i 1.
Superpozicija
Kada se kubit meri, rezultat će i dalje biti ili 0 ili 1, ali verovatnoća dobijanja određenog stanja zavisi od pravca u kom strelica pokazuje.
Ako je strelica više usmerena nagore, veća je verovatnoća da će rezultat merenja biti 1 nego 0. Ako je usmerena nadole, verovatnije je da će rezultat biti 0. Ukoliko je strelica tačno u ekvatorijalnom položaju, svako stanje će biti izmereno sa verovatnoćom od 50%.
Ovo je objašnjenje efekta superpozicije. Sada ćemo preći na pojam preplitanja.
Preplitanje
Kod klasičnih računara, bitovi su potpuno nezavisni jedni od drugih. Stanje jednog bita ne utiče na stanje drugog. Međutim, kod kvantnih računara, kubiti mogu da se prepletu jedni sa drugima, formirajući jedinstveno, veliko kvantno stanje.
Uzmimo za primer dva kubita, svaki u različitom stanju superpozicije, ali još uvek nepovezana. Uz svaki kubit možemo videti verovatnoću njegovog stanja. Ove verovatnoće su u ovom trenutku nezavisne jedna od druge.
Međutim, kada se kubiti prepletu, moramo odbaciti te nezavisne verovatnoće i izračunati raspodelu verovatnoća za sva moguća stanja u kojima se sistem može naći, tj. 00, 01, 10 ili 11.
Bitno je da su kubiti prepleteni. Ako promenite smer strelice na jednom kubitu, to će promeniti raspodelu verovatnoća za ceo sistem. Kubiti više nisu nezavisni, već su deo jednog, zajedničkog stanja.
Ovo važi bez obzira na broj kubita u sistemu. Takođe, primetićete da jedan kubit ima raspodelu verovatnoća u 2 stanja.
Dva kubita imaju raspodelu verovatnoća u četiri stanja. Tri kubita imaju raspodelu verovatnoća u osam stanja, a broj stanja se udvostručuje sa svakim dodatnim kubitom.
Uopšteno govoreći, kvantni računar sa n kubita može biti u kombinaciji od 2n stanja. Ovo je ključna razlika između klasičnih i kvantnih računara.
Klasični računari mogu biti u bilo kojem od ovih stanja, ali samo u jednom u datom trenutku, dok kvantni računari mogu istovremeno biti u superpoziciji svih ovih stanja.
Možda se pitate kako boravak u ovakvom stanju superpozicije može biti koristan pri računanju. Za to je neophodan i poslednji deo slagalice: interferencija.
Interferencija
Da bismo objasnili efekat interferencije, moramo se vratiti na vizualizaciju kubita, tehnički poznatu kao Blohova sfera. Kubit u stvarnosti ne izgleda tako. Ovo je samo vizuelno pomagalo za razumevanje stanja kubita.
U stvarnosti, stanje kubita opisuje apstraktniji entitet poznat kao kvantna talasna funkcija. Talasne funkcije su osnovni matematički opis svih pojava u kvantnoj mehanici.
Kada je više kubita prepleteno, sve njihove talasne funkcije se kombinuju u jednu, ukupnu talasnu funkciju koja opisuje stanje kvantnog računara.
Ovo kombinovanje talasnih funkcija je interferencija. Slično talasima na vodi, kada se talasi kombinuju, oni mogu konstruktivno interferirati i pojačati se ili destruktivno interferirati i poništiti se.
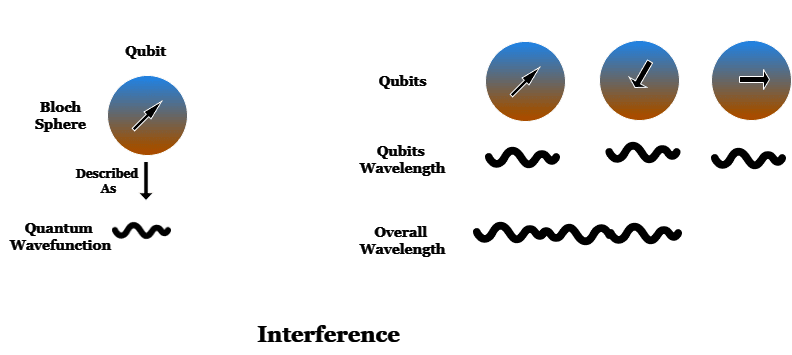
Ukupna talasna funkcija kvantnog računara određuje verovatnoće različitih stanja. Promenom stanja različitih kubita, menjamo i verovatnoće detekcije različitih stanja kada se izvrši merenje kvantnog računara.
Iako kvantni računar može biti u superpoziciji miliona stanja istovremeno, pri merenju se dobija samo jedno stanje.
Zato, pri rešavanju problema pomoću kvantnog računara, potrebno je iskoristiti konstruktivnu interferenciju kako bi se povećala verovatnoća dobijanja tačnog odgovora, a destruktivnu kako bi se smanjila verovatnoća pogrešnih odgovora. Na taj način, prilikom merenja, izlazi tačan odgovor.
Kvantni algoritmi
Način na koji se to radi je oblast kvantnih algoritama. Osnovna ideja kvantnog računarstva je da, teoretski, postoji veliki broj problema koji se mogu rešiti na kvantnom računaru, a smatra se da su nerešivi na klasičnim računarima.
Pogledajmo neke od njih. Postoji mnogo kvantnih algoritama, previše da bi se svi opisali u ovom tekstu. Stoga ćemo se fokusirati samo na najpoznatiji i istorijski najvažniji: Šorov algoritam.
#1. Šorov algoritam
Ako pomnožite dva velika broja, postoji veoma brz i efikasan klasičan algoritam za pronalaženje rezultata. Međutim, ako krenete od rezultata i pitate se koji su originalni brojevi koji su pomnoženi da bi se dobio taj rezultat, to je mnogo teže.
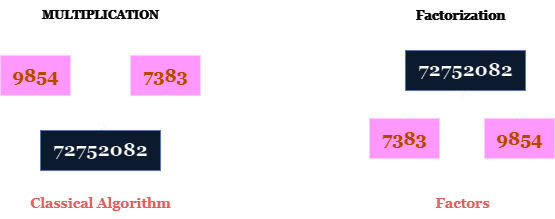
Ovo je poznato kao faktorizacija. Brojevi koji se množe se nazivaju faktori. Poteškoća u pronalaženju faktora leži u ogromnom prostoru mogućih rešenja. Ne postoji efikasan klasičan algoritam za faktorizaciju velikih brojeva.
Zbog ove matematičke osobenosti, faktorizacija se koristi za internet enkripciju: zaštitu web sajtova, email-ova i bankarskih računa. Ako znate faktore, možete lako dešifrovati informacije. Međutim, ako ih ne znate, prvo ćete ih morati naći, a taj proces je nerešiv na najmoćnijim računarima na svetu.
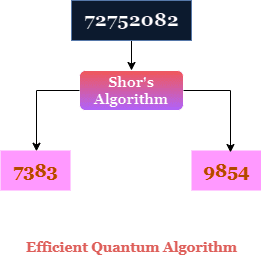Šorov algoritam
Zato je 1994. godine, kada je Piter Šor objavio brzi kvantni algoritam koji efikasno pronalazi faktore velikih celih brojeva, to izazvalo veliku pometnju.
Ovo je bio trenutak kada su mnogi ljudi počeli ozbiljno da razmatraju ideju kvantnog računarstva jer je to bila prva praktična primena, sa potencijalno ogromnim implikacijama na bezbednost u stvarnom svetu.
Ali, kada kažem ‘brzi’ kvantni algoritam, koliko bi to zaista bilo brzo i koliko brže od klasičnog računara? Da bismo odgovorili na ova pitanja, moramo malo da se pozabavimo teorijom kvantne složenosti.
Teorija kvantne složenosti
Teorija kvantne složenosti je podoblast teorije složenosti računarstva. Bavi se kategorizacijom algoritama, svrstavajući ih u grupe prema tome koliko efikasno rade na računarima.
Klasifikacija se zasniva na rastućem nivou težine rešavanja problema kako on postaje sve veći. U tom kontekstu, svaki problem unutar grupe P se lako rešava na klasičnim računarima. Međutim, sve van te grupe znači da nemamo efikasne klasične algoritme za njihovo rešavanje. Faktorizacija velikih brojeva je jedan od tih problema.
Postoji i grupa BQP, koja predstavlja probleme koji se efikasno rešavaju na kvantnim računarima, ali ne i na klasičnim. To su problemi za koje su kvantni računari superiorni u odnosu na klasične.
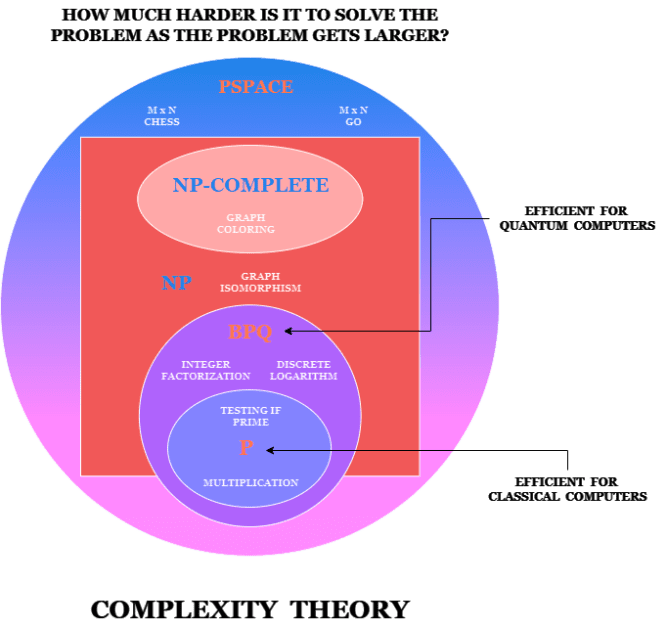
Kao što sam pomenuo, teorija složenosti razmatra koliko je teško rešiti problem, kako problem postaje sve veći. Ako faktorizujete broj od 8 cifara, a zatim dodate još jednu cifru, koliko je teže faktorizovati novi broj u poređenju sa starim? Da li je duplo teže?
Eksponencijalno teže? Kakav je trend dok dodajete sve više cifara? To se naziva složenošću ili skaliranjem, a za faktorizaciju je eksponencijalno.
Sve što ima ‘N’ u eksponentu je eksponencijalno teško. Takvi problemi su veliki izazov kako problemi postaju veći. U svetu računarstva, možete steći poštovanje i slavu ako pronađete bolji algoritam za rešavanje ovih najtežih problema.
Jedan od primera toga je bio Šorov algoritam. On koristi specifične karakteristike kvantnih računara da kreira algoritam koji može da reši problem faktorizacije celih brojeva sa skaliranjem mnogo boljim od najboljeg klasičnog algoritma.
Najbolji klasični algoritam ima eksponencijalnu složenost, dok je Šorov algoritam polinomski. To je velika stvar u teoriji složenosti i računarstvu uopšte, jer prevodi nerešiv problem u rešiv.
Rešivo, pod uslovom da imate funkcionalan kvantni računar, na čemu se trenutno radi. Ipak, još uvek ne morate da brinete o sigurnosti svojih bankovnih računa. Današnji kvantni računari nisu u stanju da pokrenu Šorov algoritam na velikim brojevima.
IBM Quantum
Za to bi bilo potrebno mnogo kubita. Trenutno, najnapredniji univerzalni kvantni računari imaju 433 kubita.
Pored toga, radi se na takozvanim post-kvantnim šemama šifrovanja, koje ne koriste faktorizaciju celih brojeva. Druga tehnologija iz kvantne fizike može pomoći u tome, kriptografska šema poznata kao kvantna kriptografija.
Ovo je bio prikaz jednog kvantnog algoritma. Postoji još mnogo, svaki sa različitim stepenom ubrzanja.
#2. Groverov algoritam
Još jedan značajan primer je Groverov algoritam, koji može brže pretraživati nestrukturirane liste podataka od najboljeg klasičnog algoritma.
Treba biti oprezan da ne prikažemo klasične računare u lošem svetlu. Oni su izuzetno raznovrsni uređaji i ne može se tvrditi da niko neće pronaći pametan klasični algoritam koji može rešiti najteže probleme kao što je faktorizacija celih brojeva.
Mnogi smatraju da je to malo verovatno, ali nije nemoguće. Takođe, postoje problemi za koje je dokazano da su nerešivi na klasičnim računarima, tzv. neizračunljivi problemi. Jedan od takvih je problem zaustavljanja. Ti problemi se ne mogu rešiti ni na kvantnim računarima.
Dakle, računarski, klasični i kvantni računari su ekvivalentni. Razlike dolaze iz algoritama koje mogu da pokreću. Čak je moguće simulirati kvantni računar na klasičnom računaru i obrnuto.
Simuliranje kvantnog računara na klasičnom postaje eksponencijalno zahtevnije sa povećanjem broja kubita koji se simuliraju.
To je zato što klasični računari teško simuliraju kvantne sisteme. Kvantni računari, koji su već kvantni sistemi, nemaju taj problem, što nas dovodi do omiljene primene kvantnih računara: kvantne simulacije.
#3. Kvantna simulacija
Kvantna simulacija koristi računare da simulira stvari poput hemijskih reakcija ili ponašanje elektrona u različitim materijalima. I ovde kvantni računari imaju eksponencijalno ubrzanje u odnosu na klasične, jer se klasični računari teško nose sa simulacijom kvantnih sistema.
Čak i simuliranje kvantnih sistema sa malim brojem čestica predstavlja izazov za najmoćnije superkompjutere na svetu. To se ne može postići ni na kvantnim računarima. Kako kvantni računari sazrevaju, glavni cilj je simuliranje sve većih kvantnih sistema.
To uključuje oblasti kao što je proučavanje ponašanja egzotičnih materijala na niskim temperaturama, razumevanje superprovodljivosti nekih materijala i proučavanje važnih hemijskih reakcija u cilju poboljšanja njihove efikasnosti. Jedan primer je proizvodnja đubriva na način koji emituje manje ugljen-dioksida, s obzirom da proizvodnja đubriva doprinosi sa oko 2% globalnih emisija ugljenika.
Možete detaljnije naučiti o simulaciji kvantne hemije.
Kvantna simulacija
Druge potencijalne primene kvantne simulacije uključuju poboljšanje solarnih panela, baterija i razvoj novih lekova, hemikalija ili materijala za vazduhoplovstvo.
Uopšteno govoreći, kvantna simulacija bi omogućila brzu izradu prototipa različitih materijala unutar kvantnog računara i testiranje njihovih fizičkih parametara, umesto da se fizički prave i testiraju u laboratoriji, što je dugotrajniji i skuplji proces.
Ovo bi značajno ubrzalo proces i rezultiralo značajnim uštedama vremena i troškova. Vredi ponoviti da su ovo sve potencijalne primene kvantnih računara, jer još uvek nemamo kvantne računare koji mogu da rešavaju probleme bolje od naših običnih računara. Međutim, ovo su problemi za koje bi kvantni računari bili idealni.
Modeli kvantnih računara
U svetu kvantnih računara, postoji veliki broj različitih pristupa za pretvaranje kvantnih sistema u kvantne računare. O tome treba da se raspravlja na dva nivoa.
Model kola
U modelu kola, kubiti rade zajedno, a specijalne kapije manipulišu sa više kubita istovremeno, menjajući njihova stanja bez provere. Postavljanjem ovih kapija u određeni redosled, kreira se kvantni algoritam. Na kraju, kubiti se mere kako bi se dobio potreban odgovor.
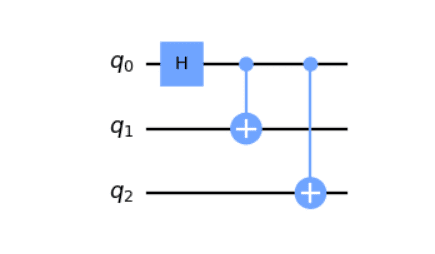Kredit za sliku: qiskit
Adijabatsko kvantno računarstvo
Kod adijabatskog kvantnog računarstva, koristi se jedno od osnovnih svojstava u fizici, a to je da se svaki sistem u fizici uvek kreće ka stanju minimalne energije. Adijabatsko kvantno računarstvo funkcioniše tako što postavlja probleme na način da najniže energetsko stanje kvantnog sistema predstavlja rešenje.
Kvantno žarenje
Kvantno žarenje nije univerzalna šema kvantnog računarstva, ali radi na istom principu kao i adijabatsko kvantno računarstvo. Sistem pronalazi stanje minimalne energije u okviru energetskog pejzaža koji mu zadate.
Topološko kvantno računarstvo
U ovom pristupu, kubiti se grade od entiteta u fizici poznatog kao Majarana nulti-mod kvazi-čestica, što je tip neabelovih anjona. Predviđa se da će ove kvazičestice biti stabilnije zbog svog fizičkog razdvajanja.
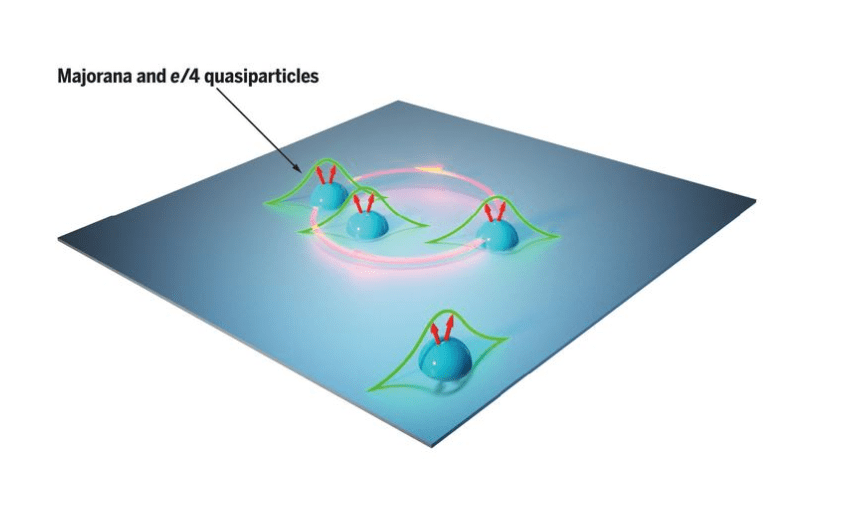Image Credit Civilsdaily
Izazovi u izgradnji
Bez obzira na pristup, svi se suočavaju sa sličnim preprekama, koje treba prvo da pogledamo.
- Dekohorencija: Veoma je teško kontrolisati kvantne sisteme. Ako postoji i najmanja interakcija sa spoljašnjim svetom, informacije počinju da cure. To se zove dekohorencija. Vaši kubiti će biti napravljeni od fizičkih stvari i biće vam potrebne druge fizičke stvari u blizini da ih kontrolišete i merite. Kubiti su osetljivi, teže da se prepletu sa svime što mogu. Potrebno je pažljivo dizajnirati kubite kako biste ih zaštitili od preplitanja sa okolinom.
- Šum: Kubite je potrebno zaštititi od bilo kakve buke, kao što su kosmički zraci, zračenje, toplotna energija ili lažne čestice. Određena količina dekohorencije i šuma je neizbežna u svakom fizičkom sistemu i nemoguće ju je u potpunosti eliminisati.
- Skalabilnost: Za svaki kubit je potreban niz žica za manipulaciju i merenje. Kako se dodaje više kubita, neophodna infrastruktura raste linearno, što predstavlja značajan inženjerski izazov. Svaki dizajn kvantnog računara mora pronaći način da efikasno uplete, kontroliše i izmeri sve kubite kako se njihov broj povećava.
- Kvantna korekcija grešaka: Kvantna korekcija grešaka je šema za ispravljanje grešaka u kvantnim računarima. Koristi se više prepletenih kubita da bi se predstavio jedan kubit bez šuma. Za kreiranje jednog kubita otpornog na greške, neophodan je veliki broj fizičkih kubita.
Fizičke implementacije
Postoji širok spektar različitih fizičkih implementacija kvantnih računara, jer postoji mnogo kvantnih sistema od kojih se oni mogu izgraditi. Evo nekih od najčešće korišćenih i najuspešnijih pristupa:
- Superprovodni kvantni računari: Superprovodni kubiti su trenutno najpopularniji pristup. Ovi kubiti se prave od superprovodnih žica sa prekidom u superprovodniku koji se zove Džozefsonov spoj. Najpopularniji tip superprovodnog kubita naziva se transmon.
- Kvantni računari sa kvantnim tačkama: Kubiti se prave od elektrona ili grupa elektrona, a sistem na dva nivoa je kodiran u spin ili naelektrisanje elektrona. Ovi kubiti se prave od poluprovodnika kao što je silicijum.
- Linearno optičko kvantno računarstvo: Optički kvantni računari koriste fotone svetlosti kao kubite i manipulišu tim kubitima koristeći optičke elemente kao što su ogledala, talasne ploče i interferometri.
- Kvantni računari sa zarobljenim jonima: Naelektrisani atomi se koriste kao kubiti. Ovi atomi su jonizovani i imaju elektron koji nedostaje. Dva stanja koja kodiraju kubit su specifični energetski nivoi atoma, kojima se može manipulisati ili ih meriti pomoću mikrotalasnog ili laserskog zraka.
- Centri za boju ili kvantni računari sa azotom: Ovi kubiti se prave od atoma ugrađenih u materijale kao što su azot u dijamantu ili silicijum karbidu. Stvaraju se pomoću nuklearnog spina ugrađenih atoma i prepliću se sa elektronima.
- Neutralni atomi u optičkim rešetkama: Ovaj pristup hvata neutralne atome u optičku rešetku, a to je ukršteni raspored laserskih zraka. Sistem od dva nivoa za kubite može biti hiperfini energetski nivo atoma ili pobuđeno stanje.
Ovo su neki od ključnih pristupa izgradnji kvantnih računara. Svaki ima svoje specifične karakteristike i izazove. Kvantno računarstvo se brzo razvija, a odabir pravog pristupa je od vitalnog značaja za budući uspeh.
Primena kvantnih računara
- Kvantna simulacija: Kvantni računari imaju potencijal da simuliraju složene kvantne sisteme, što omogućava proučavanje hemijskih reakcija, ponašanja elektrona u materijalima i različitih fizičkih parametara. Ovo se može iskoristiti za poboljšanje solarnih panela, baterija, razvoj lekova, vazduhoplovnih materijala i drugo.
- Kvantni algoritmi: Algoritmi kao što su Šorov i Groverov mogu da reše probleme koji se smatraju nerešivim za klasične računare. Nalaze primenu u kriptografiji, optimizaciji složenih sistema, mašinskom učenju i veštačkoj inteligenciji.
- Sajber bezbednost: Kvantni računari predstavljaju pretnju klasičnim sistemima šifrovanja. Međutim, oni takođe mogu doprineti sajber bezbednosti kroz razvoj kvantno otpornih šema šifrovanja. Kvantna kriptografija, oblast vezana za kvantno računarstvo, može poboljšati bezbednost.
- Problemi optimizacije: Kvantni računari mogu efikasnije rešavati složene probleme optimizacije od klasičnih računara. Ovo se može primeniti u različitim industrijama, od upravljanja lancima snabdevanja do finansijskog modeliranja.
- Vremenska prognoza i klimatske promene: Iako nisu detaljno opisane u tekstu, kvantni računari bi potencijalno mogli poboljšati modele vremenske prognoze i pomoći u rešavanju izazova povezanih sa klimatskim promenama. To je oblast koja bi mogla imati koristi od kvantnog računarstva u budućnosti.
- Kvantna kriptografija: Kvantna kriptografija povećava bezbednost podataka koristeći kvantne principe za sigurnu komunikaciju. U vreme sve većih sajber pretnji, ovo je od presudne važnosti.
Moramo biti pažljivi sa preteranim očekivanjima, jer mnoge tvrdnje o tome za šta će kvantni računari biti dobri dolaze od ljudi koji aktivno prikupljaju novac za njihovu izgradnju.
Moje mišljenje je da se istorijski pokazalo da kada se pojavi nova tehnologija, ljudi tog vremena nisu najbolji u predviđanju za šta će se koristiti.
Na primer, ljudi koji su izmislili prve računare nisu mogli ni sanjati o internetu i svim njegovim mogućnostima. Verovatno će isto važiti i za kvantne računare.
Završne misli
Kvantni računari su svakim danom sve bolji. Iako još uvek ne možemo da ih koristimo u svakodnevnom životu, imaju potencijal za praktičnu primenu u budućnosti.
U ovom tekstu smo diskutovali o različitim aspektima kvantnih računara, uključujući njihove temeljne koncepte, kao što su superpozicija, preplitanje i interferencija.
Nakon toga, istražili smo kvantne algoritme, uključujući Šorov i Groverov. Takođe smo se bavili teorijom kvantne složenosti i različitim modelima kvantnih računara.
Potom smo se bavili izazovima i praktičnim pitanjima implementacije u vezi sa kvantnim računarstvom. Na kraju, ispitali smo širok spektar potencijalnih primena kvantnih računara.
U nastavku možete pročitati i odgovore na često postavljana pitanja o kvantnom računarstvu.