Proces pretrage može biti izazovan, ali nikako nije nemoguć.
U realnom životu, pretraga se često odvija bez utvrđenog obrasca. Jednostavno idemo na mesta za koja pretpostavljamo da bi mogla sadržati ono što tražimo. U većini situacija, ne pratimo nikakav poseban redosled.
Da li isti pristup funkcioniše i u svetu programiranja?
Ne, ne funkcioniše! U programiranju postoje određeni obrasci za pretraživanje podataka. U ovom tekstu ćemo se upoznati sa nekoliko algoritama koji primenjuju različite strategije pretrage.
Postoji veliki broj algoritama za pretraživanje koji se koriste u programiranju. Mi ćemo ovde obraditi one najvažnije i najčešće korišćene. Kada razumete ove osnovne algoritme, ostale ćete lakše savladati.
U ovom tekstu, pretraga će se odnositi na pronalaženje elementa unutar niza.
Pogledajmo ove algoritme jedan po jedan.
Linearna pretraga
Kao što samo ime govori, algoritam linearne pretrage koristi linearan pristup za pretraživanje elemenata u nizu. Algoritam započinje pretragu od početka niza i nastavlja do kraja, sve dok ne pronađe traženi element. Kada pronađe element, izvršavanje programa se zaustavlja.
Da bismo bolje razumeli ovaj algoritam, pogledajmo nekoliko ilustracija.
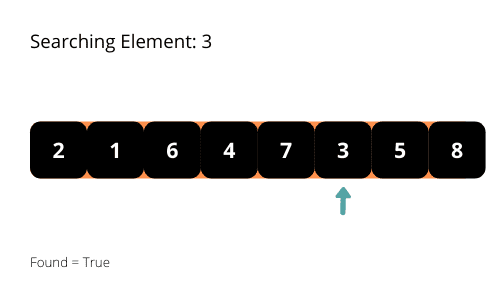
Ako pažljivo analiziramo način na koji se vrši pretraga, primetićemo da u najgorem slučaju, vreme potrebno za izvršavanje programa raste linearno sa veličinom niza, što se označava kao O(n). Vremensku složenost algoritma analiziramo u najgorem slučaju. Stoga, vremenska složenost linearne pretrage iznosi O(n).
Hajde da vidimo kako se implementira algoritam linearne pretrage.
Implementacija linearne pretrage
Sada kada razumete princip rada linearne pretrage, vreme je da se pozabavimo konkretnim kodom. Prvo ćemo definisati korake za implementaciju, a zatim ćemo pokušati da ga kodiramo. Ne brinite ako ne uspete odmah; kod ću vam dati kasnije.
Pogledajmo korake potrebne za implementaciju algoritma linearne pretrage.
- Inicijalizujte niz elemenata (recimo, vaši omiljeni brojevi).
- Napišite funkciju pod nazivom `search_element`, koja prihvata tri argumenta: niz, dužinu niza i element koji se traži.
- `search_element(arr, n, element)`:
- Prođite kroz sve elemente niza.
- Za svaki element, proverite da li je jednak traženom elementu.
- Ako jeste, vratite `True`.
- Ako se petlja završi a funkcija nije vratila `True`, to znači da traženi element nije pronađen u nizu. Vratite `False`.
- Prođite kroz sve elemente niza.
- Ispišite poruku na osnovu povratne vrednosti funkcije `search_element`.
Sada pokušajte da napišete kod na osnovu ovih koraka da biste implementirali algoritam linearne pretrage.
Jeste li završili implementaciju? Nadam se da jeste. Ako jeste, proverite svoj kod sa kodom koji sledi.
Ako niste uspeli, ne brinite; pogledajte kod ispod i videćete kako se implementira. Biće vam jasno vrlo brzo.
## Funkcija za pretragu def search_element(arr, n, element): ## Prolazimo kroz niz for i in range(n): ## Proveravamo trenutni element sa traženim elementom if arr[i] == element: ## Vraćamo True ako se poklapa return True ## Element nije pronađen, izvršavanje dolazi ovde return False if __name__ == '__main__': ## Inicijalizacija niza, dužine niza i elementa koji se traži arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 6 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "je pronađen") else: print(element_to_be_searched, "nije pronađen")
Prvo pokrenite program sa elementom koji postoji u nizu. Zatim pokrenite program sa elementom koji nije u nizu.
Vremenska složenost linearne pretrage je O(n).
Možemo li to malo poboljšati korišćenjem drugačijeg obrasca?
Da, možemo. Da vidimo kako.
Binarna pretraga
Algoritam binarne pretrage uvek prvo proverava srednji element niza. Ovaj algoritam se koristi za pretragu elemenata u sortiranom nizu.
Binarna pretraga prolazi kroz niz, proveravajući srednji element. Ako se srednji element poklapa sa traženim, program se zaustavlja. U suprotnom, ako je srednji element manji od traženog, algoritam ignoriše levi deo niza od srednjeg elementa u nastavku pretrage. Ako je srednji element veći od traženog, algoritam ignoriše desni deo niza u nastavku pretrage.
U svakoj iteraciji, algoritam binarne pretrage smanjuje prostor pretrage za polovinu. Zbog toga je ukupan broj provera manji nego kod linearne pretrage.
Ilustracije nam mogu pomoći da bolje razumemo kako radi binarna pretraga. Pogledajmo ih.
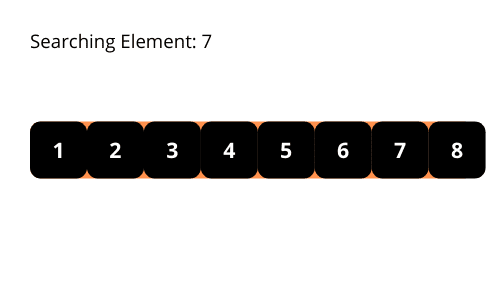
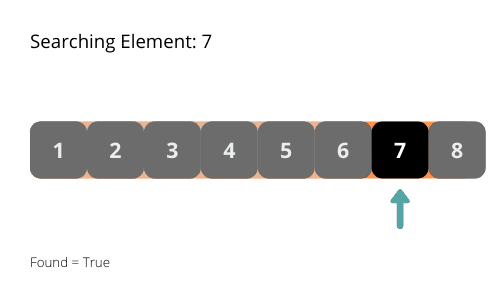
Vremenska složenost binarne pretrage je O(log n). U svakoj iteraciji, dužina prostora pretrage se smanjuje za polovinu. Smanjenje je eksponencijalno.
Implementacija binarne pretrage
Prvo ćemo pogledati korake za implementaciju binarne pretrage, a zatim i sam kod. Pogledajmo korake za implementaciju ovog algoritma.
- Inicijalizujte niz elemenata (vaši omiljeni brojevi), koji mora biti sortiran.
- Napišite funkciju pod nazivom `search_element` koja prihvata tri argumenta: sortirani niz, dužinu niza i element koji se traži.
- `search_element(sorted_arr, n, element)`:
- Inicijalizujte indeksnu promenljivu `i` za iteraciju kroz niz.
- Zatim inicijalizujte dve promenljive koje će čuvati granice prostora pretrage. Nazovimo ih `start` i `end` jer predstavljaju indekse.
- Iterirajte dok `i` ne bude manje od dužine niza.
- Izračunajte srednji indeks prostora pretrage pomoću `start` i `end` vrednosti. Formula je (`start` + `end`) // 2.
- Proverite da li je element na srednjem indeksu u prostoru pretrage jednak traženom elementu.
- Ako jeste, vratite `True`.
- Inače, ako je element na srednjem indeksu manji od traženog elementa, pomerite početni indeks prostora pretrage na `middle` + 1.
- Inače, ako je element na srednjem indeksu veći od traženog elementa, pomerite krajnji indeks prostora pretrage na `middle` – 1.
- Povećajte indeks niza `i`.
- Ako se petlja završi i izvršavanje je još u funkciji, to znači da element nije pronađen u nizu. Vratite `False`.
- Ispišite poruku na osnovu povratne vrednosti funkcije `search_element`.
Pokušajte da napišete kod, slično implementaciji algoritma linearne pretrage.
…
Da li ste dobili kod?
Uporedite ga sa kodom ispod. Ako niste, ne brinite; razumećete implementaciju uz pomoć ovog koda.
## Funkcija za pretragu def search_element(sorted_arr, n, element): ## Indeks niza za iteraciju i = 0 ## Promenljive za praćenje prostora pretrage ## Inicijalizacija sa početnim i krajnjim indeksima start = 0 end = n - 1 ## Iteriramo kroz niz while i < n: ## Dobijamo indeks srednjeg elementa middle = (start + end) // 2 ## Proveravamo da li je srednji element jednak traženom if sorted_arr[middle] == element: ## Vraćamo True ako je element pronađen return True elif sorted_arr[middle] < element: ## Pomeramo početni indeks prostora pretrage udesno start = middle + 1 else: ## Pomeramo krajnji indeks prostora pretrage ulevo end = middle - 1 i += 1 return False if __name__ == '__main__': ## Inicijalizacija niza, dužine niza i elementa koji se traži arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 9 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "je pronađen") else: print(element_to_be_searched, "nije pronađen")
Testirajte kod sa različitim slučajevima, kako kada je element prisutan, tako i kada nije.
Zaključak
Binarni algoritam pretrage je mnogo efikasniji od algoritma linearne pretrage. Međutim, binarna pretraga zahteva da niz bude sortiran, što nije slučaj sa linearnom pretragom. Sortiranje troši određeno vreme. Upotreba efikasnog algoritma za sortiranje u kombinaciji sa binarnom pretragom predstavlja dobar pristup.
Sada imate osnovno znanje o najčešće korišćenim algoritmima pretrage u Pythonu.
U nastavku se informišite o nekim popularnim softverima za pretragu koje možete sami hostovati.
Srećno sa kodiranjem 🙂 🧑💻