Ovaj vodič će vas uputiti kako da ispišete Paskalov trougao u programskom jeziku Python za određeni broj redova.
Započećete sa učenjem kako se konstruiše Paskalov trougao. Potom ćete preći na pisanje Python funkcije i naučiti kako da je dodatno optimizujete.
▶ Krenimo!
Šta je Paskalov trougao i kako ga konstruisati?
Ispisivanje Paskalovog trougla za dati broj redova je popularan zadatak na intervjuima za posao.
U Paskalovom trouglu koji ima ‘n’ redova, red broj ‘i’ sadrži ‘i’ elemenata.
Dakle, prvi red ima jedan element, a to je broj 1. Svaki element u narednim redovima predstavlja zbir dva broja koji se nalaze direktno iznad njega.
Sledeća ilustracija objašnjava proces konstruisanja Paskalovog trougla sa pet redova.
Paskalov trougao za broj redova = 5 (Slika autora)
Obratite pažnju na to kako se mogu dodati nule kada imate samo jedan broj iznad određenog mesta.
📝 Kao brzu vežbu, ponovite gore opisani postupak da biste konstruisali Paskalov trougao za n = 6 i n = 7.
Nakon toga, pređimo na pisanje koda. Možete koristiti vdzzvdz-ov Python IDE direktno u svom internet pretraživaču dok prolazite kroz ovaj vodič.
Python funkcija za ispisivanje Paskalovog trougla
U ovom odeljku ćemo napisati Python funkciju koja ispisuje Paskalov trougao za bilo koji zadati broj redova.
Postoje dva ključna pitanja na koja treba obratiti pažnju:
- Kako predstaviti unose u Paskalovom trouglu?
- Kako ispisati Paskalov trougao sa odgovarajućim razmacima i formatiranjem?
Hajde da odgovorimo na njih odmah.
#1. Koji izraz predstavlja svaki unos u Paskalovom trouglu?
Ispostavlja se da se unosi u Paskalov trougao mogu izračunati pomoću formule za nCr. Ako se sećate matematike iz škole, nCr označava broj načina na koji možete izabrati ‘r’ stavki iz skupa od ‘n’ stavki.
Formula za nCr je data u nastavku:
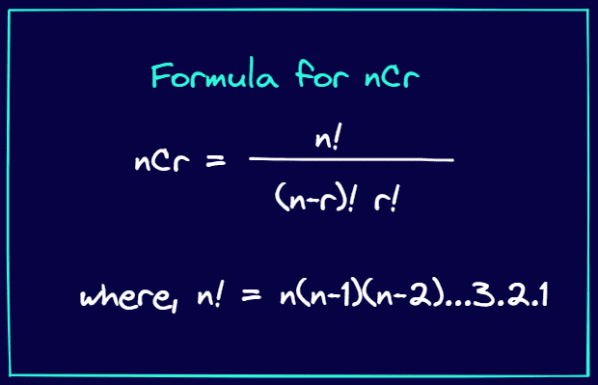nCr formula (Slika autora)
Sada nastavimo da izražavamo unose u Paskalovom trouglu koristeći nCr formulu.
Paskalovi unosi trougla koristeći nCr (Slika autora)
Sada smo pronašli način da izrazimo unose u matrici.
#2. Kako podesiti razmake prilikom ispisivanja šablona?
U Paskalovom trouglu sa numRows, red #1 ima jedan unos, red #2 ima dva unosa, i tako dalje. Da biste ispisali obrazac u obliku trougla, biće vam potrebno numRows – i razmaka u redu #i. Možete koristiti Python funkciju range u kombinaciji sa for petljom da biste to uradili.
Pošto funkcija range po default-u isključuje krajnju tačku, obavezno dodajte + 1 da biste dobili potreban broj razmaka na početku.
Sada kada ste naučili kako da predstavite unose i prilagodite razmak prilikom ispisa Paskalovog trougla, hajde da definišemo funkciju pascal_tri.
Analiza definicije funkcije
Dakle, šta treba da radi funkcija pascal_tri?
- Funkcija pascal_tri treba da prihvati broj redova (numRows) kao argument.
- Treba da ispiše Paskalov trougao sa numRows redova.
Da bismo izračunali faktorijel, koristimo funkciju factorial iz Python-ovog ugrađenog matematičkog modula.
▶ Pokrenite sledeći blok koda da biste uvezli factorial i koristili ga u trenutnom modulu.
from math import factorial
Isečak koda ispod sadrži definiciju funkcije.
def pascal_tri(numRows):
'''Ispisuje Paskalov trougao sa numRows redova.'''
for i in range(numRows):
# petlja za dobijanje razmaka na početku reda
for j in range(numRows-i+1):
print(end=" ")
# petlja za dobijanje elemenata reda i
for j in range(i+1):
# nCr = n!/((n-r)!*r!)
print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")
# ispisuje svaki red u novom redu
print("n")
Funkcija radi na sledeći način:
- Funkcija pascal_tri ima jedan obavezan parametar numRows: broj redova.
- Ukupno ima numRows redova. Za svaki red ‘i’ dodajemo numRows – i razmaka na početku pre prvog unosa u redu.
- Zatim koristimo formulu nCr za izračunavanje pojedinačnih unosa. Za red ‘i’, unosi su iCj gde je j = {0,1,2,..,i}.
- Obratite pažnju na to da koristimo //, koji vrši celobrojno deljenje, jer želimo da unosi budu celi brojevi.
- Nakon izračunavanja svih unosa u redu, štampamo sledeći red u novom redu.
🔗 Pošto smo dodali docstring, možete koristiti Python-ovu ugrađenu funkciju help ili atribut __doc__ da biste pristupili nizu dokumenta funkcije. Isečak koda ispod pokazuje kako se to radi.
help(pascal_tri)
# Output
Help on function pascal_tri in module __main__:
pascal_tri(numRows)
Ispisuje Paskalov trougao sa numRows redova.
pascal_tri.__doc__
# Output
Ispisuje Paskalov trougao sa numRows redova.
Hajde sada da pozovemo funkciju sa brojem redova kao argumentom.
pascal_tri(3)
# Output
1
1 1
1 2 1
Prva 3 reda Paskalovog trougla su ispisana, kao što se i očekivalo.
Ispisivanje Paskalovog trougla pomoću rekurzije
U prethodnom odeljku smo identifikovali matematički izraz svakog unosa u Paskalovom trouglu. Međutim, nismo iskoristili odnos između unosa u dva uzastopna reda.
Zapravo, koristili smo prethodni red da bismo izračunali unose u sledećem redu. Možemo li to iskoristiti i smisliti rekurzivnu implementaciju funkcije pascal_tri?
Da, uradimo to!
U rekurzivnoj implementaciji, funkcija više puta poziva samu sebe dok se ne ispuni osnovni slučaj. U konstrukciji Paskalovog trougla, počinjemo od prvog reda sa jednim unosom 1, a zatim gradimo sledeće redove.
Dakle, poziv funkcije pascal_tri(numRows) zauzvrat poziva pascal_tri(numRows-1) i tako dalje, sve dok se ne dostigne osnovni slučaj pascal_tri(1).
Razmotrite primer gde treba da ispišete prva 3 reda Paskalovog trougla. Sledeća slika objašnjava kako se rekurzivni pozivi guraju na stek. I kako rekurzivni pozivi funkcije vraćaju redove Paskalovog trougla.
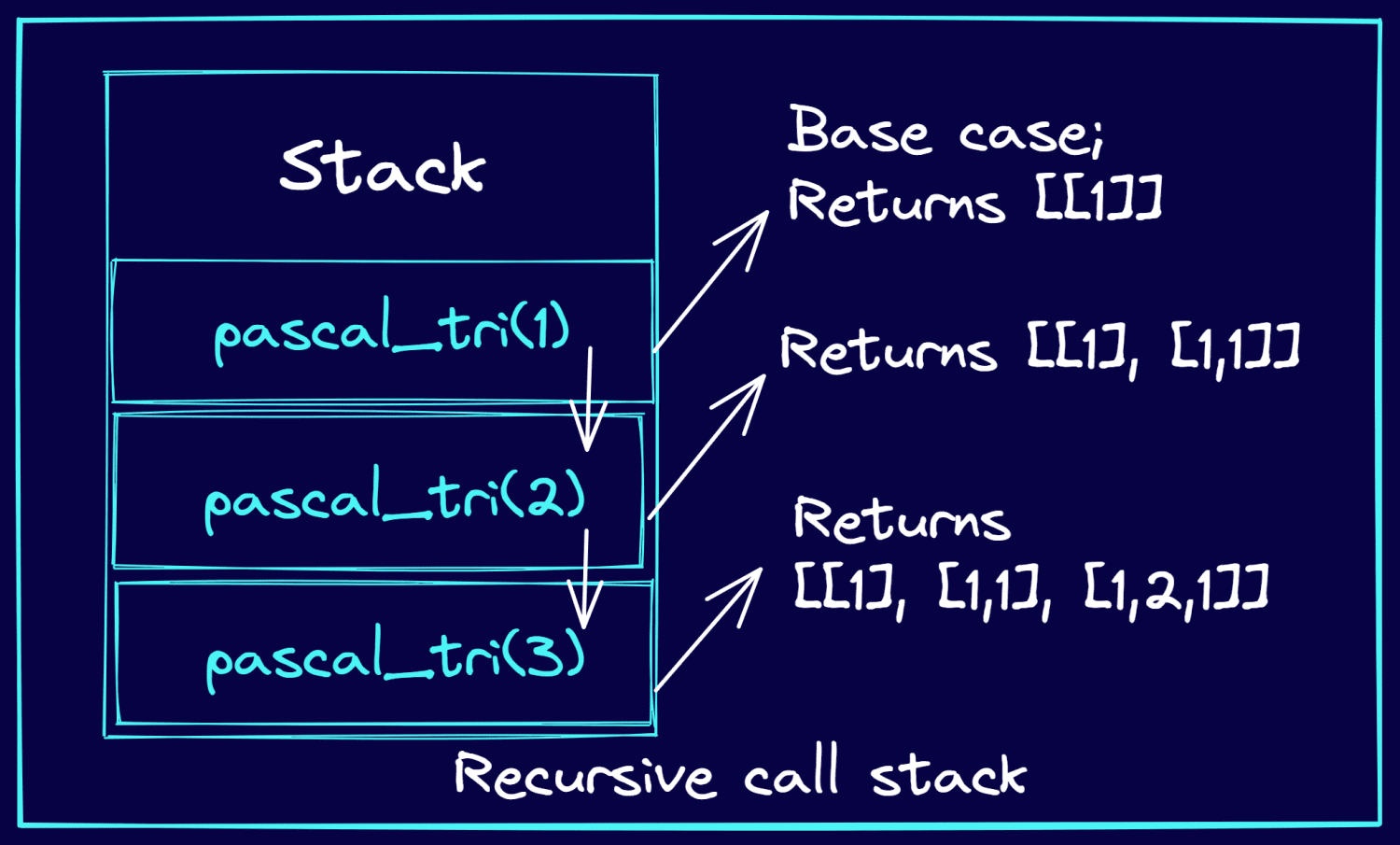Grupa poziva tokom rekurzivnih poziva (Slika autora)
▶ Pokrenite isečak koda ispod da generišete redove Paskalovog trougla rekurzivno.
def pascal_tri(numRows):
'''Ispisuje Paskalov trougao sa numRows redova.'''
if numRows == 1:
return [[1]] # osnovni slučaj
else:
res_arr = pascal_tri(numRows-1) # rekurzivni poziv funkcije pascal_tri
# korišćenje prethodnog reda za izračunavanje trenutnog reda
cur_row = [1] # svaki red počinje sa 1
prev_row = res_arr[-1]
for i in range(len(prev_row)-1):
# zbir 2 elementa direktno iznad
cur_row.append(prev_row[i] + prev_row[i+1])
cur_row += [1] # svaki red se završava sa 1
res_arr.append(cur_row)
return res_arr
Evo nekoliko tačaka na koje vredi obratiti pažnju:
- Koristili smo ugnežđenu listu kao strukturu podataka, gde je svaki red u Paskalovom trouglu lista za sebe, ovako: [[red 1], [red 2],…,[red n]].
- Poziv funkcije pascal_tri(numRows) pokreće seriju rekurzivnih poziva sa numRows – 1, numRows – 2 sve do 1 kao argumentima. Ovi pozivi se guraju na stek.
- Kada je numRows == 1, došli smo do osnovnog slučaja i funkcija vraća [[1]].
- Sada vraćenu listu koriste sledeće funkcije u steku poziva—za izračunavanje sledećeg reda.
- Ako je cur_row trenutni red, cur_row[i] = prethodni_red[i] + prethodni_red[i+1]—zbir 2 elementa direktno iznad trenutnog indeksa.
Pošto je vraćeni niz ugnežđena lista (lista lista), moramo da prilagodimo razmak i ispišemo unose, kao što je prikazano u bloku koda ispod.
tri_array = pascal_tri(5)
for i,row in enumerate(tri_array):
for j in range(len(tri_array) - i + 1):
print(end=" ") # razmaci na početku
for j in row:
print(j, end=" ") # štampanje elemenata
print("n") # štampanje novog reda
Izlaz je tačan, kao što se vidi ispod!
# Output
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Python funkcija za ispisivanje Paskalovog trougla za broj redova ≤ 5
Oba metoda koja ste naučili će raditi na ispisivanju Paskalovog trougla za proizvoljan broj redova numRows.
Međutim, postoje situacije kada je potrebno da ispišete Paskalov trougao za manji broj redova. A kada je broj redova koji treba da ispišete najviše 5 — možete koristiti jednostavnu tehniku.
Pogledajte ilustraciju ispod. I posmatrajte kako su stepeni broja 11 identični unosima u Paskalovom trouglu. Takođe, primetite da ovo funkcioniše samo do 4. stepena od 11. To jest, 11 podignuto na stepene {0, 1, 2, 3, 4} daje unose u redovima od 1 do 5 Paskalovog trougla.
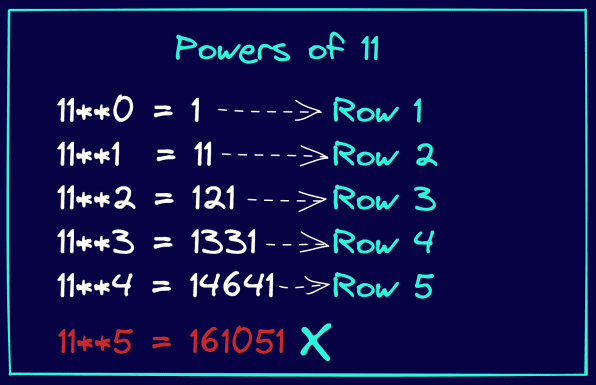
Hajde da ponovo napišemo definiciju funkcije, kao što je prikazano u nastavku:
def pascal_tri(numRows):
'''Ispisuje Paskalov trougao sa numRows redova.'''
for i in range(numRows):
print(' '*(numRows-i), end='')
# izračunava stepen broja 11
print(' '.join(str(11**i)))
Evo kako funkcioniše funkcija pascal_tri:
- Kao i u prethodnim primerima, prilagođavamo razmak.
- Zatim koristimo Python-ov operator eksponencijacije (**) da bismo izračunali stepene broja 11.
- Pošto su stepeni broja 11 po default-u celi brojevi, konvertujemo ih u string pomoću str(). Sada imamo stepene broja 11 kao stringove.
- Stringovi u Python-u su iterabilni—tako da možete proći kroz njih i pristupiti jednom po jednom znaku.
- Zatim možete koristiti metod join() sa sintaksom:
.join( ) da biste spojili elemente u koristeći kao separator. - Ovde vam je potreban jedan razmak između znakova, tako da će
biti ‘ ‘, a je string: stepen broja 11.
Hajde da proverimo da li funkcija radi kako treba.
pascal_tri(5)
# Output
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Kao drugi primer, pozovite funkciju pascal_tri sa 4 kao argumentom.
pascal_tri(4)
# Output
1
1 1
1 2 1
1 3 3 1
Nadam se da sada znate kako možete lako da ispišete Paskalov trougao za numRows u opsegu od 1 do 5.
Zaključak
Evo šta smo naučili:
- Kako konstruisati Paskalov trougao sa datim brojem redova. Svaki broj u svakom redu je zbir dva broja direktno iznad njega.
- Napisali smo Python funkciju koristeći formulu nCr = n!/(n-r)!.r! za izračunavanje unosa Paskalovog trougla.
- Zatim ste naučili rekurzivnu implementaciju funkcije.
- Na kraju, naučili ste najoptimalniji metod za konstruisanje Paskalovog trougla za broj redova do 5—korišćenjem stepena broja 11.
Ako želite da unapredite svoje Python veštine, naučite kako da množite matrice, proverite da li je broj prost i rešavate probleme sa string operacijama. Srećno sa kodiranjem!