Ovaj vodič će vas uputiti kako da kreirate Python program koji proverava da li je određeni broj prost ili ne.
Ukoliko ste se ikada susreli sa zadacima na testovima kodiranja, verovatno ste naišli na matematičko pitanje koje se tiče provere primarnosti, odnosno utvrđivanja da li je broj prost. U narednim minutima, naučićete kako da dođete do efikasnog rešenja za ovaj problem.
U ovom vodiču ćete:
- ponoviti osnove o prostim brojevima,
- napisati Python kod za proveru da li je broj prost, i
- optimizovati ga radi postizanja O(√n) algoritma vremena izvršavanja.
Za sve navedeno, hajde da počnemo.
Šta je prost broj?
Započnimo sa pregledom osnovnih karakteristika prostih brojeva.
U teoriji brojeva, prirodan broj n se smatra prostim ako ima tačno dva delioca: 1 i sam taj broj (n). Podsetimo se iz školskih dana: broj i je delilac broja n ukoliko i deli n bez ostatka. ✅
Sledeća tabela prikazuje nekoliko brojeva, sve njihove delioce i da li su prosti.
| n | Delioci | Da li je prost? |
| 1 | 1 | Ne |
| 2 | 1, 2 | Da |
| 3 | 1, 3 | Da |
| 4 | 1, 2, 4 | Ne |
| 7 | 1, 7 | Da |
| 15 | 1, 3, 5, 15 | Ne |
Iz gornje tabele možemo uočiti sledeće:
- 2 je najmanji prost broj.
- 1 je delilac svakog broja.
- Svaki broj n je sam sebi delilac.
Dakle, 1 i n su takozvani trivijalni delioci za bilo koji broj n. Prost broj ne bi trebalo da ima druge delioce osim ova dva.
To znači da kada prelazite sa 2 na n – 1, ne bi trebalo da pronađete netrivijalnog delioca koji deli n bez ostatka.
O(n) algoritam za proveru da li je broj prost u Pythonu
U ovom odeljku, formalizujmo navedeni pristup u Python funkciji.
Možete proći kroz sve brojeve od 2 do n – 1 koristeći `range()` objekat u Pythonu.
U Pythonu, `range(start, stop, step)` vraća objekat opsega. Zatim, možete iterirati kroz taj objekat da biste dobili niz brojeva počevši od `start` pa sve do `stop – 1` u koracima veličine `step`.
S obzirom da nam je potreban skup celih brojeva od 2 do n – 1, možemo navesti `range(2, n)` i koristiti ga zajedno sa `for` petljom.
Evo šta bismo želeli da uradimo:
- Ako pronađete broj koji deli n bez ostatka, možete odmah zaključiti da broj nije prost.
- Ako prođete kroz ceo opseg brojeva od 2 do n – 1 a da niste pronašli broj koji deli n bez ostatka, onda je broj prost.
Python funkcija za proveru da li je broj prost
Na osnovu gore navedenog, možemo definisati funkciju `is_prime()` na sledeći način.
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
Sada, analizirajmo gornju definiciju funkcije.
- Gornja funkcija `is_prime()` uzima pozitivan ceo broj `n` kao argument.
- Ako pronađete delioca u navedenom opsegu od (2, n-1), funkcija vraća `False`—jer broj nije prost.
- I vraća `True` ako se prođe kroz celu petlju bez pronalaženja delioca.
Zatim, pozovimo funkciju sa različitim argumentima i proverimo da li je izlaz tačan.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
U gornjem izlazu, vidite da su 2 i 11 prosti brojevi (funkcija vraća `True`). A 8 i 9 nisu prosti (funkcija vraća `False`).
Kako optimizovati Python funkciju `is_prime()`
Ovde možemo izvršiti manju optimizaciju. Obratite pažnju na listu delioca u tabeli ispod.
| Broj | Delioci |
| 6 | 1, 2, 3, 6 |
| 10 | 1, 2, 5, 10 |
| 18 | 1, 2, 3, 6, 9, 18 |
Možemo videti da je jedini delilac od n koji je veći od n/2 sam n.
To znači da ne moramo da prelazimo kroz petlju sve do n – 1. Umesto toga, možemo pokrenuti petlju samo do n/2.
Ako ne pronađemo netrivijalnog delioca do n/2, nećemo ga pronaći ni posle n/2.
Hajde sada da modifikujemo funkciju `is_prime()` da proverava delioce u opsegu (2, n/2).
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
Proverimo sada izlaz kroz nekoliko poziva funkcije.
is_prime(9) # False is_prime(11) # True
Iako se može činiti da smo optimizovali, ovaj algoritam nije efikasniji od prethodnog u smislu složenosti vremena izvršavanja. Oba imaju O(n) složenost vremena izvršavanja, što je proporcionalno vrednosti n ili linearno u n.
Možemo li bolje? Da, možemo!
▶ Pređite na sledeći odeljak da biste saznali kako da poboljšamo vremensku složenost za testiranje prostih brojeva.
O(√n) algoritam za proveru da li je broj prost u Pythonu
Ispostavlja se da se delioci broja pojavljuju u parovima.
Ako je a delilac broja n, onda postoji i delilac b takav da je a * b = n, ili jednostavno, ab = n.
Proverimo ovo na primeru.
Tabela ispod prikazuje delioce broja 18 koji se pojavljuju u parovima. Možete potvrditi ovo za još nekoliko brojeva ako želite.
Takođe, imajte na umu da je √18 približno 4.24.
U parovima delioca (a, b), možete videti da ako je a manje od 4.24, onda je b veće od 4.24—u ovom primeru, (2, 9) i (3, 6).
| Faktori 18 u parovima |
| (1, 18) |
| (2, 9) |
| (3, 6) |
Ako je broj n savršen kvadrat, imaćete a = b = √n kao jedan od delilaca.
▶ Pogledajte delioce od 36 u tabeli ispod. Pošto je 36 savršen kvadrat, a = b = 6 je jedan od delilaca. Za sve ostale parove delilaca (a, b) važi a < 6 i b > 6.
| Faktori 36 u parovima |
| (1, 36) |
| (2, 18) |
| (3, 12) |
| (4, 9) |
| (6, 6) |
U sumi, imamo sledeće:
- Svaki broj n se može napisati kao n = a * b
- Ako je n savršen kvadrat, onda je a = b = √n.
- Ako je a < b, onda je a < √n i b > √n.
- U suprotnom, ako je a > b, onda je a > √n i b < √n.
Dakle, umesto da prolazite kroz sve cele brojeve do n/2, možete odabrati da prođete samo do √n. Ovo je znatno efikasnije od našeg prethodnog pristupa.
Kako modifikovati `is_prime()` u O(√n) algoritam
Hajde da optimizujemo funkciju za proveru prostih brojeva u Pythonu.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
Sada, analizirajmo gornju definiciju funkcije:
- Da bismo izračunali kvadratni koren broja, uvozimo Python-ov ugrađeni `math` modul i koristimo funkciju `math.sqrt()`.
- Pošto n možda nije savršen kvadrat, moraćemo da ga pretvorimo u ceo broj. Koristite `int(var)` da prebacite `var` u `int`.
- Da bismo bili sigurni da zaista proveravamo do √n, dodajemo plus jedan pošto funkcija `range()` po default-u isključuje krajnju tačku opsega.
Kod ispod potvrđuje da naša funkcija `is_prime()` radi ispravno.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
U sledećem odeljku, napravimo nekoliko jednostavnih dijagrama da bismo vizuelno razumeli O(n) i O(√n).
Poređenje O(n) i O(√n) vizuelno
▶ Pokrenite sledeći isječak koda u okruženju Jupyter notebook po svom izboru.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
Gornji isječak pokazuje kako možete nacrtati krive za n i √n za određeni opseg vrednosti.
- Koristimo funkciju NumPy `arange()` da kreiramo niz brojeva.
- A zatim prikupljamo vrednosti n i √n do, ali ne uključujući 20, u pandas DataFrame.
- Zatim crtamo koristeći Seaborn’s `lineplot()` funkciju.
Iz grafikona ispod vidimo da je √n znatno manje od n.
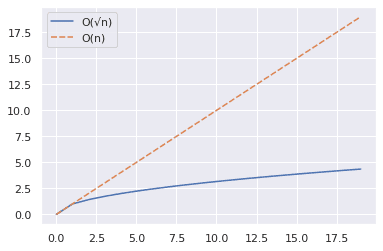
Sada, hajde da povećamo opseg na 2000 i ponovimo iste korake kao gore.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
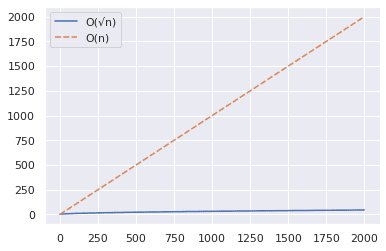
Iz gornjeg dijagrama možete zaključiti da je O(√n) algoritam znatno brži kada testirate da li je veliki broj prost.
Evo kratkog primera: 2377 je prost broj—potvrdite ovo!😀
Dok će O(n) pristup imati redosled od 2000 koraka, O(√n) algoritam može pomoći da se dođe do odgovora u samo 49 koraka.✅
Zaključak
⏳ Vreme je za kratak rezime.
- Da biste proverili da li je broj prost, naivan pristup je da se prođe kroz sve brojeve u opsegu (2, n-1). Ako ne pronađete delioca koji deli n, onda je n prost.
- Pošto je jedini delilac od n veći od n/2 sam n, možete odabrati da prođete samo do n/2.
- Oba gornja pristupa imaju vremensku složenost od O(n).
- Pošto se delioci broja pojavljuju u parovima, možete proći samo do √n. Ovaj algoritam je mnogo brži od O(n). A dobitak je primetan kada se proverava da li je veliki broj prost ili ne.
Nadam se da razumete kako da proverite da li je broj prost u Pythonu. Kao sledeći korak, možete pogledati naš vodič o Python programima o operacijama sa stringovima — gde ćete naučiti da proverite da li su stringovi palindromi, anagrami i još mnogo toga.
Vidimo se u drugom tutorijalu. Do tada, srećno kodiranje!👩🏽💻