U svetu programiranja, strukture podataka imaju ključnu ulogu. One omogućavaju efikasno organizovanje informacija, čineći ih lakšim za korišćenje. Stek je jedna od najjednostavnijih i najvažnijih struktura.
Hajde da detaljnije istražimo stek i vidimo kako se implementira u programskom jeziku Python.
Šta je stek?
Stek se može uporediti sa gomilom knjiga, stolica ili bilo kojih drugih predmeta koji su naslagani jedan na drugi u stvarnom životu. Karakteriše ga princip „poslednji ušao, prvi izašao“ (LIFO – Last In, First Out). Ovo je zaista jedna od najosnovnijih struktura podataka. Razmotrimo jedan primer iz stvarnog života:
Zamislite da imamo gomilu knjiga, postavljenu jednu na drugu.
Ako želimo da uzmemo treću knjigu odozgo, moraćemo prvo ukloniti prve dve knjige. U ovom slučaju, knjiga koja je poslednja stavljena na gomilu, prva će biti uzeta sa gomile. Stek kao struktura podataka u programiranju prati isti princip – LIFO.
Operacije sa stekom
U osnovi, postoje dve glavne operacije koje se mogu izvršavati nad stekom:
1. push(podatak)
Ova operacija dodaje, tj. „gura“ novi podatak na vrh steka.
2. pop()
Ova operacija uklanja, tj. „izbacuje“ podatak koji se nalazi na vrhu steka.
Na slici ispod možete videti ilustracije push i pop operacija.
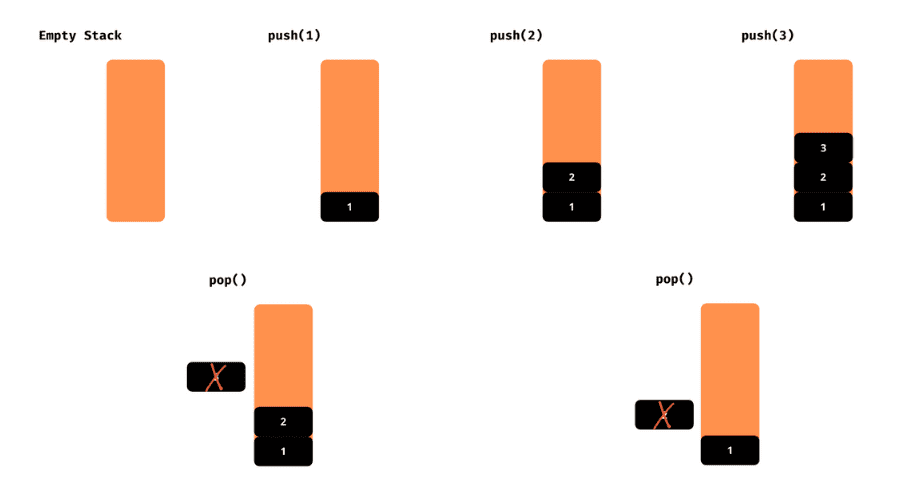
Napisaćemo i nekoliko pomoćnih funkcija koje će nam pružiti dodatne informacije o stanju steka.
Evo o kojim pomoćnim funkcijama je reč:
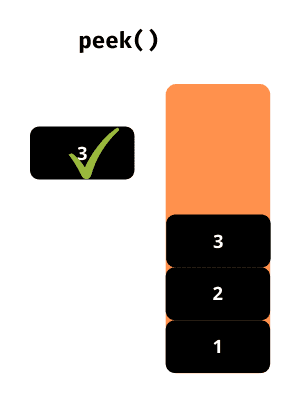
peek()
Ova funkcija vraća podatak koji se nalazi na samom vrhu steka, bez njegovog uklanjanja.
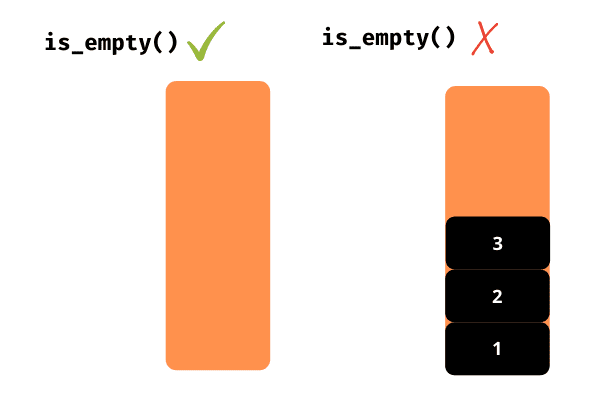
isEmpty()
Ova funkcija proverava da li je stek prazan i vraća odgovarajući rezultat (true ili false).
Sada kada smo razjasnili konceptualne aspekte steka, pređimo na njegovu implementaciju, bez daljeg odlaganja.
Pretpostavljam da imate instaliran Python na vašem računaru. Ako to nije slučaj, možete koristiti i neki online kompajler.
Implementacija steka
Implementacija steka je, u poređenju sa drugim strukturama podataka, relativno jednostavna. U Pythonu postoji nekoliko načina za implementaciju steka.
Razmotrićemo ih sve, jedan po jedan.
#1. Lista
Stek ćemo implementirati koristeći listu unutar klase. Hajde da vidimo korak po korak implementaciju steka:
Korak 1: Kreirajte klasu pod nazivom „Stack“.
class Stack:
pass
Korak 2: Potrebno je da podatke skladištimo u listi. Dodajmo praznu listu unutar klase „Stack“, pod imenom „elements“.
class Stack:
def __init__(self):
self.elements = []
Korak 3: Da bismo mogli da dodajemo elemente na stek, potreban nam je metod. Napravimo metod „push“ koji prima podatak kao argument i dodaje ga na listu „elements“.
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
Korak 4: Slično, hajde da napišemo „pop“ metod, koji uklanja element sa vrha steka. Možemo koristiti ugrađeni „pop“ metod za tip podatka lista.
class Stack:
## ...
def pop(self):
return self.elements.pop()
Završili smo osnovnu implementaciju steka sa neophodnim operacijama. Sada ćemo dodati i pomoćne funkcije kako bismo dobili više informacija o steku.
Korak 5: Možemo dobiti element sa vrha steka korišćenjem negativnog indeksa. Element koda [-1] vraća poslednji element liste, što je, u našem slučaju, element na vrhu steka.
class Stack:
## ...
def peek(self):
return self.elements[-1]
Korak 6: Ako je dužina liste „elements“ jednaka 0, to znači da je stek prazan. Napravimo metod koji vraća informaciju o tome da li je stek prazan ili ne.
class Stack:
## ...
def is_empty(self):
return len(self.elements) == 0
Završili smo implementaciju steka koristeći tip podatka „lista“.
Čekajte malo! Upravo smo implementirali stek, ali kako ga koristiti? Kako da ga testiramo?
Da vidimo kako se to radi. Prvo moramo kreirati objekat klase „Stack“ da bismo ga mogli koristiti. Nije ništa komplikovano, uradimo to odmah.
class Stack:
## ...
if __name__ == '__main__':
stack = Stack()
Napravili smo objekat steka i sada smo spremni da ga koristimo. Pratimo sledeće korake da testiramo operacije steka:
- Proverite da li je stek prazan ili ne, pomoću metode „is_empty“. Rezultat bi trebalo da bude „True“.
- Dodajte brojeve 1, 2, 3, 4 i 5 na stek pomoću metode „push“.
- Metoda „is_empty“ bi sada trebalo da vrati „False“. Proverite.
- Ispišite element sa vrha steka koristeći metodu „peek“.
- Izbacite element sa vrha steka pomoću metode „pop“.
- Ponovo proverite element sa vrha steka pomoću metode „peek“. Rezultat bi trebalo da bude 4.
- Sada izbacite sve elemente sa steka.
- Metoda „is_empty“ bi trebalo da vrati „True“. Proverite.
Ako su svi navedeni koraci uspešno izvršeni, to znači da smo uspešno implementirali stek. Pokušajte da sami napišete kod za ove korake.
Da li ste napisali kod? Ako niste, nema problema, pogledajte kod ispod:
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
def pop(self):
return self.elements.pop()
def peek(self):
return self.elements[-1]
def is_empty(self):
return len(self.elements) == 0
if __name__ == '__main__':
stack = Stack()
## checking is_empty method -> true
print(stack.is_empty())
## pushing the elements
stack.push(1)
stack.push(2)
stack.push(3)
stack.push(4)
stack.push(5)
## again checking is_empty method -> false
print(stack.is_empty())
## printing the topmost element of the stack -> 5
print(stack.peek())
## popping the topmost element -> 5
stack.pop()
## checking the topmost element using peek method -> 4
print(stack.peek())
## popping all the elements
stack.pop()
stack.pop()
stack.pop()
stack.pop()
## checking the is_empty method for the last time -> true
print(stack.is_empty())
Uspeli smo! Implementirali smo stek od nule, koristeći tip podatka „lista“. Ukoliko pokrenete gornji kod, dobićete izlaz kao što je navedeno u nastavku:
True False 5 4 True
Možemo direktno koristiti listu kao stek. Međutim, ova implementacija je dobra za razumevanje kako se stek implementira i u drugim programskim jezicima.
Takođe, možete pogledati i ove članke koji se odnose na listu.
Hajde da sada vidimo ugrađeni „deque“ iz modula „collections“, koji takođe može poslužiti kao stek.
#2. deque iz „collections“
„Deque“ je implementiran kao dvostrani red. Budući da podržava dodavanje i uklanjanje elemenata sa oba kraja, može se koristiti kao stek. Možemo ga podesiti da poštuje LIFO princip steka.
Implementiran je korišćenjem druge strukture podataka koja se zove dvostruko povezana lista. Zato su performanse umetanja i brisanja elemenata konzistentne. Pristup elementima sa sredine dvostruko povezane liste traje O(n) vremena. Međutim, možemo ga koristiti kao stek, jer nema potrebe za pristupom srednjim elementima steka.
Pre same implementacije steka, pogledajmo metode koje se koriste za implementaciju steka pomoću reda:
- append(podatak) – koristi se za dodavanje podatka na vrh steka
- pop() – koristi se za uklanjanje elementa sa vrha steka
Ne postoje direktne zamene za metode „peek“ i „is_empty“. Umesto „peek“, možemo ispisati ceo stek. Za proveru da li je stek prazan, možemo koristiti „len“ metod.
Implementirajmo stek koristeći „deque“ iz modula „collections“.
from collections import deque ## creating deque object stack = deque() ## checking whether stack is empty or not -> true print(len(stack) == 0) ## pushing the elements stack.append(1) stack.append(2) stack.append(3) stack.append(4) stack.append(5) ## again checking whether stack is empty or not -> false print(len(stack) == 0) ## printing the stack print(stack) ## popping the topmost element -> 5 stack.pop() ## printing the stack print(stack) ## popping all the elements stack.pop() stack.pop() stack.pop() stack.pop() ## checking the whether stack is empty or not for the last time -> true print(len(stack) == 0)
To je to! Naučili smo kako da implementiramo stek koristeći „deque“ iz modula „collections“. Ukoliko pokrenete gornji program, dobićete izlaz kao što je navedeno ispod:
True False deque([1, 2, 3, 4, 5]) deque([1, 2, 3, 4]) True
Do sada smo videli dva načina za implementaciju steka. Postoje li i drugi načini? Da! Hajde da vidimo još jedan, poslednji način za implementaciju steka u ovom vodiču.
#3. LifoQueue
Sam naziv „LifoQueue“ govori da ova klasa sledi LIFO princip. Zbog toga je možemo bez problema koristiti kao stek. Ona dolazi iz modula „queue“. „LifoQueue“ pruža nekoliko korisnih metoda koje su od pomoći prilikom implementacije steka. Da vidimo koje su to metode:
- put(podatak) – dodaje, tj. „gura“ podatak u red
- get() – uklanja, tj. „izbacuje“ element sa vrha reda
- empty() – vraća informaciju da li je red prazan ili ne
- qsize() – vraća dužinu reda
Implementirajmo stek koristeći „LifoQueue“ iz modula „queue“.
from queue import LifoQueue
## creating LifoQueue object
stack = LifoQueue()
## checking whether stack is empty or not -> true
print(stack.empty())
## pushing the elements
stack.put(1)
stack.put(2)
stack.put(3)
stack.put(4)
stack.put(5)
## again checking whether stack is empty or not -> false
print(stack.empty())
## popping all the elements
print(stack.get())
print(stack.get())
print(stack.get())
## checking the stack size
print("Size", stack.qsize())
print(stack.get())
print(stack.get())
## checking the whether stack is empty or not for the last time -> true
print(stack.empty())
Ukoliko pokrenete gornji program bez izmena, dobićete sledeći izlaz:
True False 5 4 3 Size 2 2 1 True
Primena steka
Sada kada posedujete dovoljno znanja o steku, možete ga primeniti i u rešavanju programerskih problema. Razmotrimo jedan problem i rešimo ga pomoću steka.
Zadat je izraz. Potrebno je napisati program koji proverava da li su zagrade, uglaste zagrade i vitičaste zagrade pravilno izbalansirane ili ne.
Razmotrimo neke primere:
Ulaz: „[{}]([])“
Izlaz: Izbalansirano
Ulaz: „{[}]([])“
Izlaz: Nije izbalansirano
Za rešavanje ovog problema možemo koristiti stek. Pogledajmo korake koje treba da pratimo:
- Kreirajte stek za čuvanje znakova.
- Ako je dužina izraza neparna, izraz nije izbalansiran.
- Prođite kroz dati izraz.
- Ako je trenutni znak početna zagrada (ili { ili [, dodajte ga na stek.
- U suprotnom, ako je trenutni znak zatvorena zagrada ) ili } ili ], izbacite element sa steka.
- Ako se izbačeni znak poklapa sa početnom zagradom, nastavite dalje. U suprotnom, zagrade nisu izbalansirane.
- Nakon iteracije, ako je stek prazan, jednačina je izbalansirana. U suprotnom, jednačina nije izbalansirana.
Možemo koristiti tip podatka „set“ za proveru da li se zagrade poklapaju.
## stack
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
def pop(self):
return self.elements.pop()
def peek(self):
return self.elements[-1]
def is_empty(self):
return len(self.elements) == 0
def balance_check(expression):
## checking the length of the expression
if len(expression) % 2 != 0:
## not balanced if the length is odd
return False
## for checking
opening_brackets = set('([{')
pairs = set([ ('(',')'), ('[',']'), ('{','}') ])
## stack initialization
stack = Stack()
## iterating through the given expression
for bracket in expression:
## checking whether the current bracket is opened or not
if bracket in opening_brackets:
## adding to the stack
stack.push(bracket)
else:
## popping out the last bracket from the stack
popped_bracket = stack.pop()
## checking whether popped and current bracket pair
if (popped_bracket, bracket) not in pairs:
return False
return stack.is_empty()
if __name__ == '__main__':
if balance_check('[{}]([])'):
print("Balanced")
else:
print("Not Balanced")
if balance_check('{[}]([])'):
print("Balanced")
else:
print("Not Balanced")
Stek se može koristiti za rešavanje mnogih drugih problema. Gore navedeni problem je samo jedan od primera. Pokušajte da primenite koncept steka kad god mislite da je to najbolje rešenje.
Zaključak
Ura! Stigli ste do kraja ovog vodiča. Nadam se da ste uživali u ovom vodiču koliko sam i ja uživao dok sam ga pravio. To je sve za ovaj tutorijal.
Srećno kodiranje 🙂 👨💻