Razvrstavanje spiskova podataka predstavlja ključni aspekt obrade informacija u okviru različitih aplikacija.
Ova operacija je izuzetno korisna za prezentovanje podataka na organizovan način i za sprovođenje efikasnih pretraga. Stoga, nije iznenađujuće da svaki kompetentan softverski inženjer mora da poseduje veštine razvrstavanja nizova. U ovom članku biće objašnjeni neki od najčešćih algoritama koji se koriste za sortiranje nizova u JavaScriptu.
Šta je sortiranje i zašto je korisno?
 Izvor: Unsplash
Izvor: Unsplash
Sortiranje je sistematsko organizovanje vrednosti prema određenom kriterijumu. Ovaj poredak može biti uzlazni ili silazni. Sortiranje nizova u JavaScriptu je korisno jer omogućava pregledniji i smisleniji prikaz podataka.
Na primer, korisnik može želeti da pregleda datoteke poređane po datumu, počevši od najnovijih, ili proizvode sortirane po ceni. Takođe, sortiranje je od suštinskog značaja za obavljanje binarne pretrage, koja funkcioniše isključivo sa sortiranom kolekcijom podataka.
Iako postoje ugrađene funkcije i biblioteke koje olakšavaju sortiranje podataka, neophodno je razumeti kako sortiranje funkcioniše „ispod haube“, naročito za potrebe intervjua za posao i kada je potrebno pisati kod niskog nivoa.
Algoritmi za sortiranje nizova u JavaScriptu
Bubble Sort

Bubble Sort je verovatno najjednostavniji algoritam za razumevanje i implementaciju. Njegov rad se zasniva na prolasku kroz niz u iteracijama. U svakoj iteraciji, krećemo se kroz niz od početka do kraja, poredeći svaka dva susedna elementa. Ukoliko su elementi u pogrešnom redosledu, vršimo zamenu njihovih pozicija.
Izvodimo ukupno n iteracija, gde je n broj elemenata u nizu. Sa svakom iteracijom, niz se postepeno sortira, počevši od desne strane. Pseudokod za algoritam sortiranja brojeva u rastućem redosledu je sledeći:
1. Neka je n broj elemenata u nizu 2. Ponavljaj n puta, brojeći iteracije pomoću promenljive i (u svakoj iteraciji izvršavaj sledeće): a. Prođi kroz niz od drugog elementa do (n-i)-tog elementa b. Ako je prethodni element veći od trenutnog elementa, zameni ih.
Prevedeno u JavaScript, kod bi izgledao ovako:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
Za bolje razumevanje procesa, preporučuje se dodavanje console.log unutar obe petlje da biste pratili kako se niz menja sa svakim prolaskom kroz petlju.
U kodu ispod, modifikovana je funkcija sortiranja kako bi se dodali console.log ispisi unutar dve petlje. Takođe, kreiran je mali, nesortirani niz koji se sortira pomoću modifikovane funkcije.
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
Rezultat izvršavanja gornjeg koda bi bio:

Bubble Sort ima veliku vremensku složenost od O(n^2). Razlog tome je što se vrši n prolaza kroz niz, a u svakom prolazu se ponovo prolazi kroz niz. Zbog toga performanse ovog algoritma nisu najsjajnije. Međutim, on ima prostornu složenost od O(1), pošto modifikuje elemente niza na istom mestu u memoriji.
Insertion Sort

Insertion Sort je popularan algoritam za sortiranje nizova u JavaScriptu. Pretpostavimo da koristimo Insertion Sort za sortiranje vrednosti u rastućem redosledu. Algoritam radi tako što se bira broj, koji ćemo nazvati num. Zatim se num pomera ulevo sve dok svaki drugi broj levo od num nije manji od tog broja. Svi brojevi će biti poređani ukoliko se ovaj postupak primeni počevši od drugog elementa do kraja niza. Evo opisa u pseudokodu.
1. Neka je n broj elemenata u nizu
2. Ponavljaj za i od 1 do n-1 (počevši od drugog elementa):
a. Postavi currentElement na array[i]
b. Postavi j na i-1
c. Dok je j >= 0 i array[j] > current_element:
i. Pomeri array[j] na array[j+1]
ii. Umanji j za 1
d. Postavi array[j+1] na current_element
A sada, pseudokod implementiran u JavaScriptu izgleda ovako.
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
Kao i kod Bubble Sort-a, dodavanje console.log ispisa pomaže u vizualizaciji onoga što se dešava. Kod ispod prikazuje Insertion Sort u praksi.
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
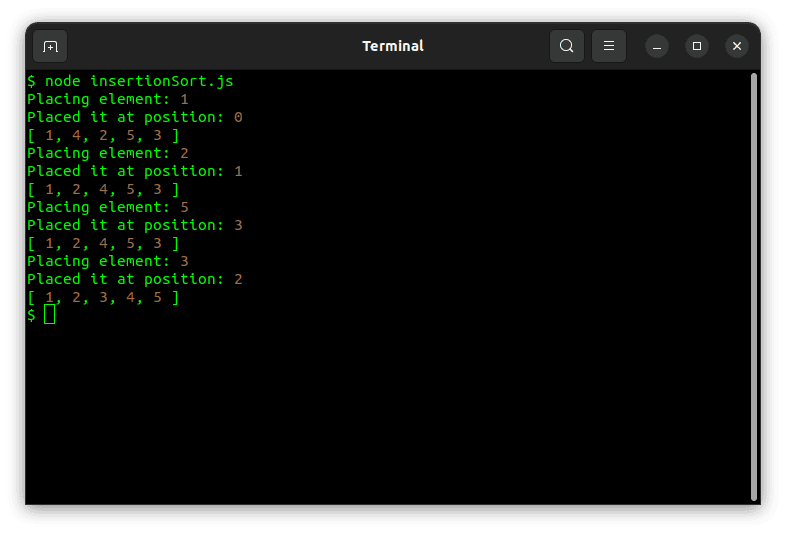
const array = [4, 1, 2, 5, 3];
sort(array);
A izvršavanje gornjeg koda daje sledeći rezultat:
Merge Sort

Dok se Insertion Sort i Bubble Sort skaliraju sa kvadratnom vremenskom složenošću, Merge Sort se skalira sa kvazilinearnom vremenskom složenošću. On ima vremensku složenost od O(n*log(n)).
Merge Sort koristi pristup „podeli pa vladaj“. Niz se uzastopno deli na manje podnizove, sve dok se ne dobiju nizovi od po jednog elementa. Nakon deljenja, ovi podnizovi se ponovo spajaju.
Podela se vrši rekurzivno, kako bi se niz na kraju ponovo sastavio.
Prilikom ponovnog spajanja podnizova, oni se spajaju sortirano. Spajanje se izvodi na isti način na koji biste spojili dva sortirana niza. Pseudokod za to je napisan u nastavku:
1. Ako je dužina niza 1 ili manja, vrati niz (bazni slučaj)
2. Odredi srednji indeks:
a. Postavi mid na ceo broj dobijen deljenjem (dužine niza / 2)
3. Podeli niz na dva podniza:
a. Kreiraj leftArray i prekopiraj prvu polovinu niza u njega (od indeksa 0 do mid)
b. Kreiraj rightArray i prekopiraj drugu polovinu niza u njega (od indeksa mid+1 do kraja)
4. Rekurzivno pozovi MergeSort na leftArray
5. Rekurzivno pozovi MergeSort na rightArray
6. Spoji dva sortirana podniza:
a. Kreiraj prazan resultArray
b. Dok leftArray i rightArray nisu prazni:
i. Ako je prvi element u leftArray manji ili jednak prvom elementu u rightArray, dodaj ga u resultArray
ii. U suprotnom, dodaj prvi element u rightArray u resultArray
c. Dodaj preostale elemente iz leftArray u resultArray (ako ih ima)
d. Dodaj preostale elemente iz rightArray u resultArray (ako ih ima)
7. Vrati resultArray
Implementacija u JavaScriptu bi izgledala ovako:
function sort(array) {
// Bazni slučaj u kojem zaustavljamo dalje deljenje niza
if (array.length == 1) {
return array;
}
// Određivanje središnje tačke niza
const m = Math.round(array.length / 2);
// Podela niza na dve polovine
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Rekurzivno pozivanje merge sort-a
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Vraćanje spojenog sortiranog niza
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Spajanje dve sortirane liste
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
Ako pokrenete ovaj kod sa primerom niza, on bi trebao ispravno da funkcioniše.
Quick Sort

Poput Merge Sort-a, Quick Sort se oslanja na pristup „podeli pa vladaj“. Algoritam bira pivot element. Zatim pomera sve elemente veće od pivota udesno, a manje od pivota ulevo. Nakon što se ovo uradi, pivot će biti na ispravnoj poziciji.
Da bi pomerio elemente oko pivota, algoritam počinje pomeranjem pivota na kraj niza.
Nakon što se on pomeri, koristimo pokazivač za prolazak kroz niz sa leve strane, tražeći prvi broj veći od pivota. Istovremeno, koristimo drugu petlju pokazivača sa desne strane niza, tražeći prvi broj manji od pivota. Kada se identifikuju oba broja, vršimo zamenu njihovih pozicija. Ovaj postupak se ponavlja sve dok pokazivač sa leve strane ne postane veći od pokazivača sa desne strane.
Kada se petlja zaustavi, zamenjujemo veći od dva poslednja broja sa pivotom. U ovom trenutku, pivot će se nalaziti na ispravnoj poziciji; brojevi manji od pivota će biti levo, dok će oni veći biti desno.
Ovaj postupak se rekurzivno ponavlja za podnizove levo i desno od pivota sve dok podnizovi nemaju samo jedan preostali element.
Evo pseudokoda za Quick Sort:
1. Ako je lessThanPointer manji od greaterThanPointer:
a. Izaberi pivot element iz niza
b. Pomeri elemente tako da budu oni koji su manji sa leve strane, a veći sa desne:
c. Rekurzivno pozovi QuickSort na leftSubarray
d. Rekurzivno pozovi QuickSort na rightSubarray
A prebacivanje u JavaScript:
function sort(array, low, high) {
if (low < high) {
// Izaberi indeks pivota i particioniši niz
const pivotIndex = move(array, low, high);
// Rekurzivno sortiraj podnizove levo i desno od pivota
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Izaberi pivot element (u ovom slučaju, poslednji element)
const pivotElement = array[high];
// Inicijalizuj indeks za manji element
let i = low - 1;
for (let j = low; j < high; j++) {
// Ako je trenutni element manji ili jednak pivotu, zameni ga sa elementom na indeksu i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Zameni pivot element na njegovu ispravnu poziciju
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Vrati indeks pivot elementa
return i + 1;
}
Sortiranje niza koristeći Quick Sort u Node.js bi trebalo dati sledeći rezultat:
U najboljem slučaju, Quick Sort radi u kvazilinearnoj vremenskoj složenosti. Korišćenje prostora u Quick Sort-u se takođe logaritamski skalira. Stoga je relativno efikasan u poređenju sa drugim algoritmima za sortiranje nizova u JavaScriptu.
Saveti za intervjue za kodiranje
❇ Vežba je ključna. Pomaže vam da naučite različite algoritme, ali što je još važnije, pomaže vam da razvijete veštine rešavanja problema i računarskog razmišljanja. Takođe možete vežbati na platformama kao što su Leetcode i AlgoExpert.
❇ Pokušajte prvo sami da rešite problem. Umesto da odmah pređete na rešenje, pokušajte da ga rešite samostalno, jer vam to pomaže da razvijete svoje veštine rešavanja problema.
❇ Ako vam rešavanje problema traje predugo, pređite na rešenje; još uvek možete naučiti kako da rešite problem iz rešenja. Većina platformi za učenje nudi rešenja. ChatGPT ili Google Bard su takođe korisni za objašnjavanje koncepata.
❇ Takođe, nemojte odmah pisati kod; prvo skicirajte vaša rešenja na papiru i razmislite o njima pre nego što napišete kod. Pseudokod je takođe koristan način za brzo zapisivanje ideja.
Zaključak
U ovom članku smo obradili najpopularnije algoritme za sortiranje. Međutim, učenje svega ovoga u početku može izgledati previše. Stoga, obično preporučujem da kombinujete različite izvore informacija umesto da se oslanjate samo na jedan. Srećno sa kodiranjem!
Zatim pogledajte kako funkcioniše sorted funkcija u Python-u.