Постоји одређена доза сумње у поузданост већине статистичких података, чак и када се придржавају свих прописаних процедура и користи најсавременија опрема. Међутим, Ексел пружа могућност израчунавања несигурности на основу стандардне девијације узорка.
У Екселу се налазе статистичке функције које омогућавају израчунавање несигурности. У овом тексту ћемо се бавити прорачуном аритметичке средине, стандардне девијације и стандардне грешке. Такође, видећемо како се ова несигурност може визуелно приказати на графикону у Екселу.
За ове прорачуне користићемо следеће узорке података.
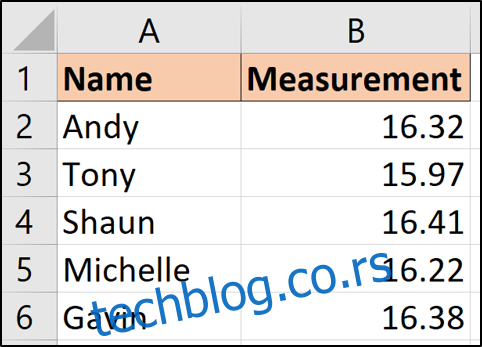
Ови подаци представљају пет особа које су извршиле мерење или очитавање неке величине. Са пет различитих очитавања, јавља се несигурност у вези са тим која је тачна вредност.
Израчунавање аритметичке средине
Када постоји несигурност због различитих вредности, просек (аритметичка средина) се може сматрати најприближнијом проценом тачне вредности.
У Екселу се то лако постиже помоћу функције АВЕРАГЕ.
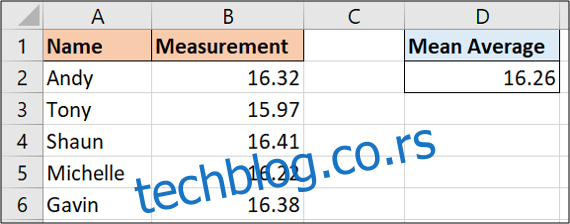
За наведене узорке података, може се употребити следећа формула:
=AVERAGE(B2:B6)
Стандардна девијација вредности
Функције за израчунавање стандардне девијације показују колико су вредности распоређене у односу на централну вредност (аритметичку средину коју смо претходно израчунали).
Ексел нуди неколико функција за стандардну девијацију за различите намене. Две основне су СТДЕВ.П и СТДЕВ.С.
Обе функције израчунавају стандардну девијацију, али је разлика у томе што се СТДЕВ.П користи када је доступан цео скуп вредности, док СТДЕВ.С ради са мањим узорком из тог скупа.
У овом примеру, користимо свих пет вредности из скупа, те ћемо се користити функцијом СТДЕВ.П.
Ова функција се користи на сличан начин као и функција АВЕРАГЕ. За наведени узорак података, може се употребити следећа формула:
=STDEV.P(B2:B6)
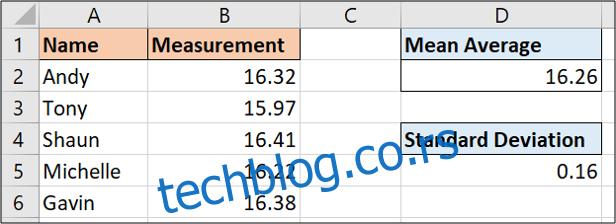
Резултат за ових пет вредности је 0,16. Ова вредност показује колико се појединачно мерење уобичајено разликује од просечне вредности.
Израчунавање стандардне грешке
Са израчунатом стандардном девијацијом, сада можемо израчунати стандардну грешку.
Стандардна грешка се добија дељењем стандардне девијације са квадратним кореном броја мерења.
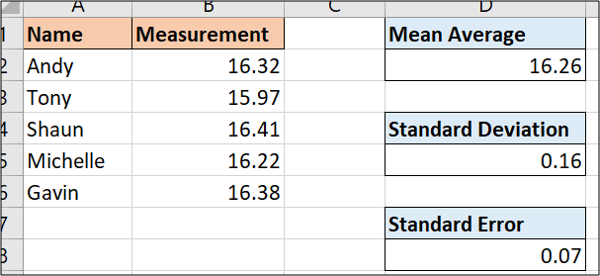
За наведене узорке података, може се употребити следећа формула:
=D5/SQRT(COUNT(B2:B6))
Приказ несигурности на графиконима помоћу трака грешке
Ексел олакшава приказ стандардних девијација или маргина несигурности на графиконима, што се постиже додавањем трака грешке.
У наставку је приказан стубичасти дијаграм из узорка података који показује популацију мерену током пет година.
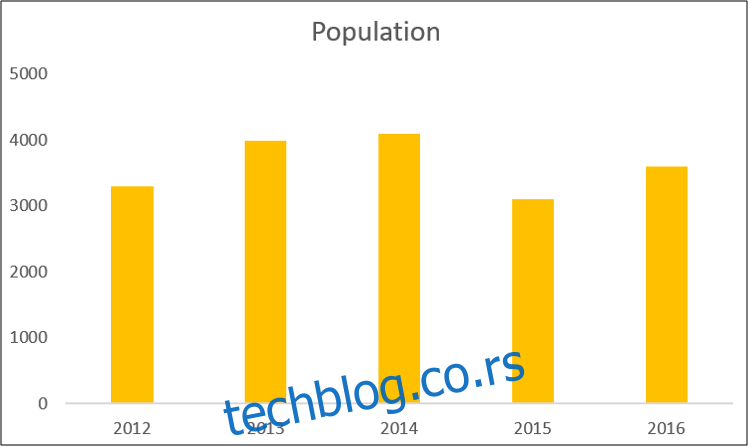
Након одабира графикона, кликните на „Дизајн“ > „Додај елемент графикона“.
Затим одаберите жељени тип трака грешке.
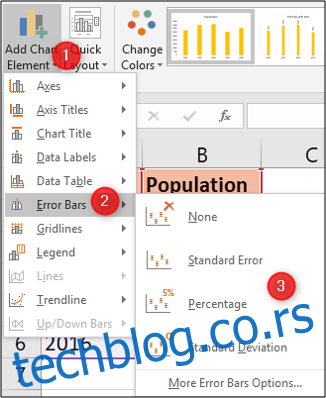
Можете приказати стандардну грешку или износ стандардне девијације за све вредности, као што смо раније израчунали. Такође је могуће приказати процентуалне промене грешке, а подразумевана вредност је 5%.
За овај пример, одабрали смо приказ процента грешке.
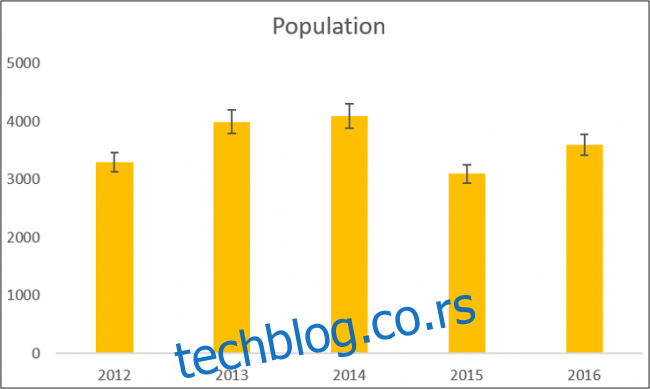
Постоје и додатне опције за прилагођавање трака грешке.
Двоструким кликом на траку грешке на графикону отвара се прозор „Форматирање трака грешке“. Ако већ није изабрана, одаберите категорију „Опције трака грешке“.
Затим можете подесити проценат, вредност стандардне девијације, или чак одабрати прилагођену вредност из ћелије која је можда добијена статистичком формулом.
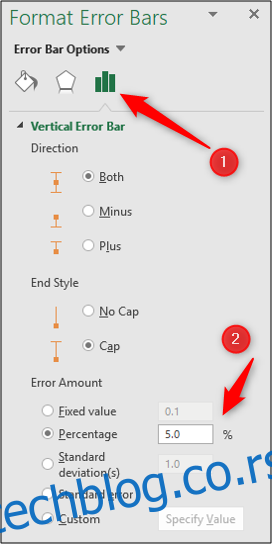
Ексел је изузетан алат за статистичку анализу и извештавање. Пружа мноштво метода за израчунавање несигурности, омогућавајући вам да добијете потребне информације.