У овом тексту ћемо истражити како се врши множење две матрице у програмском језику Python.
Прво ћемо се позабавити условима који морају бити испуњени да би множење матрица било могуће, и направићемо Python функцију која имплементира множење матрица. Затим ћемо видети како се исти резултат може постићи користећи уграђене листе.
На крају, искористићемо могућности NumPy библиотеке и њене функције за ефикасније множење матрица.
Провера ваљаности множења матрица
Пре него што почнемо са писањем Python кода за множење матрица, подсетимо се основних правила.
Множење матрица A и B је могуће само ако је број колона матрице A једнак броју редова матрице B.
Могуће је да сте се већ сусретали са овим условом. Међутим, да ли сте се икада питали зашто је то тако?
Разлог лежи у самом процесу множења матрица. Погледајте илустрацију испод.
У општем случају, матрица A има m редова и n колона, док матрица B има n редова и p колона.
Облик резултујуће матрице
Елемент на позицији (i, j) у резултујућој матрици C представља скаларни производ i-тог реда матрице A и j-те колоне матрице B.
Дакле, за израчунавање елемента на одређеној позицији у матрици C, неопходно је израчунати скаларни производ одговарајућег реда и колоне у матрицама A и B.
Понављањем овог процеса, добијамо резултујућу матрицу C димензија m x p – са m редова и p колона, као што је приказано испод.
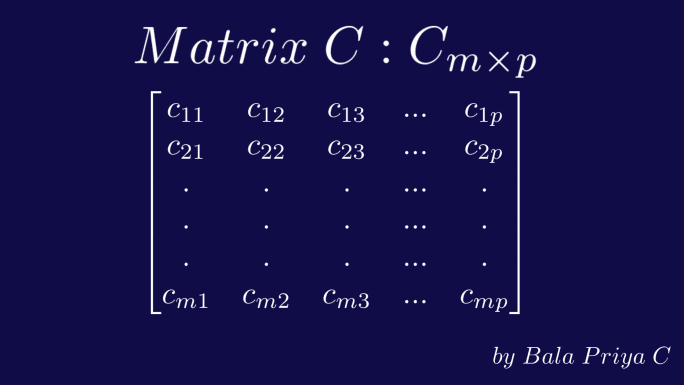
Скаларни или унутрашњи производ два вектора a и b се израчунава по следећој формули:

Да резимирамо:
- Скаларни производ је дефинисан само између вектора исте дужине.
- За скаларни производ између реда и колоне – током множења две матрице – неопходно је да оба имају исти број елемената.
- У претходном примеру, сваки ред матрице A има n елемената, као и свака колона матрице B.
n представља број колона у матрици A, а такође и број редова у матрици B. Отуда и услов да број колона матрице A мора бити једнак броју редова матрице B.
Надам се да је сада јасан услов ваљаности множења матрица и начин израчунавања елемената резултујуће матрице.
Сада можемо почети са писањем Python кода за множење матрица.
Креирање прилагођене Python функције за множење матрица
Прво, написаћемо прилагођену функцију за множење матрица.
Ова функција треба да:
- Прима две матрице, A и B, као улазне вредности.
- Провери да ли је множење матрица A и B ваљано.
- Уколико је ваљано, помножи матрице A и B и врати резултујућу матрицу C.
- У супротном, врати поруку о грешци да матрице A и B није могуће помножити.
Корак 1: Креирајмо две матрице целих бројева користећи NumPy функцију random.randint(). Такође, можете дефинисати матрице као уграђене листе у Python-у.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Matrix A:n {A}n")
print(f"Matrix B:n {B}n")
# Output
Matrix A:
[[4 9 9]
[9 1 6]
[9 2 3]]
Matrix B:
[[2 2]
[5 7]
[4 4]]
Корак 2: Дефинишимо функцију multiply_matrix(A,B). Ова функција прима две матрице A и B као улазне параметре и враћа матрицу производа C уколико је множење матрица ваљано.
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(rows):
for col in range(cols):
for elt in range(len(B)):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "Sorry, cannot multiply A and B."
Анализа дефиниције функције
Сада ћемо детаљније анализирати дефиницију функције.
Декларисање C као глобалне променљиве: Подразумевано, променљиве унутар Python функције имају локални опсег и не могу се користити ван функције. Да би резултујућа матрица C била доступна и ван функције, морамо је декларисати као глобалну променљиву. То се постиже коришћењем кључне речи global пре имена променљиве.
Провера ваљаности множења матрица: Користимо атрибут shape да проверимо могућност множења A и B. За било који низ arr, arr.shape[0] и arr.shape[1] враћају број редова и колона, респективно. Услов A.shape[1] == B.shape[0] проверава ваљаност множења матрица. Само ако је овај услов испуњен, израчунава се матрица производа. У супротном, функција враћа поруку о грешци.
Употреба угнежђених петљи за израчунавање вредности: Да бисмо израчунали елементе резултујуће матрице, пролазимо кроз редове матрице A користећи спољашњу for петљу. Унутрашња for петља служи за пролазак кроз колоне матрице B. Најдубља for петља нам омогућава приступ сваком елементу у одабраној колони.
▶ Сада када разумемо како функционише Python функција за множење матрица, позваћемо је са матрицама A и B које смо претходно генерисали.
multiply_matrix(A,B)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Пошто је множење матрица A и B ваљано, функција multiply_matrix() враћа матрицу производа C.
Множење матрица користећи уграђене листе у Python-у
У претходном делу, написали смо Python функцију за множење матрица. Сада ћемо видети како се исти резултат може постићи користећи уграђене листе.
Ово је начин на који се користи уграђена листа за множење матрица:
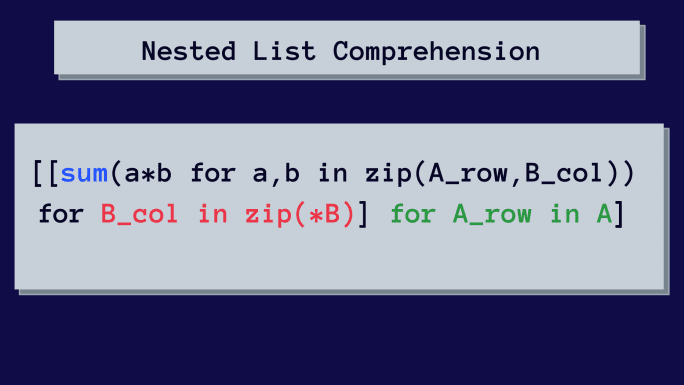
На први поглед, ово може изгледати компликовано. Међутим, анализираћемо уграђену листу корак по корак.
Фокусираћемо се на сваку листу понаособ и утврдити шта она ради.
Користићемо следећи шаблон за уграђене листе:
[<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through
▶ Погледајте наш водич Разумевање листе у Питхон-у – са примерима да бисте стекли дубинско разумевање.
Пре него што наставимо, важно је запамтити да желимо да креирамо резултујућу матрицу C ред по ред.
Објашњење уграђених листа
Корак 1: Израчунавање појединачне вредности у матрици C
За дати ред i матрице A и колону j матрице B, следећи израз враћа унос на позицији (i, j) у матрици C.
sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on
Ако је i = j = 1, израз ће вратити унос c_11 матрице C. На овај начин, можемо добити један елемент у једном реду.
Корак 2: Креирање једног реда у матрици C
Следећи циљ нам је да направимо цео ред.
За ред 1 у матрици A, морамо проћи кроз све колоне матрице B да бисмо добити један комплетан ред у матрици C.
Вратимо се на шаблон за разумевање листе.
- Заменимо
<do-this>са изразом из корака 1, јер је то оно што желимо да урадимо. - Затим, заменимо
<item>са B_col – сваком колоном матрице B. - Коначно, заменимо
<iterable>саzip(*B)– листом која садржи све колоне матрице B.
И ево прве листе:
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B
Корак 3: Креирање свих редова и добијање матрице C
Затим, потребно је попунити матрицу производа C израчунавањем преосталих редова.
За ово морамо проћи кроз све редове матрице A.
Вратимо се на разумевање листе и урадимо следеће:
- Заменимо
<do-this>са листом из корака 2. Подсетимо се да смо у претходном кораку израчунали један цео ред. - Сада заменимо
<item>са A_row – сваким редом у матрици A. <iterable>је матрица A сама по себи, јер пролазимо кроз њене редове.
И ево наше коначне уграђене листе.🎊
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
Време је да проверимо резултат! ✔
# cast into <a href="https://techblog.co.rs.com/numpy-reshape-arrays-in-python/">NumPy array</a> using np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Output:
[[ 89 107]
[ 47 49]
[ 40 44]]
Ако боље погледамо, ово је еквивалентно угнежђеним for петљама које смо имали претходно – само што је сажетије.
Ово можемо учинити још ефикасније користећи неке уграђене функције. Сазнаћемо више о њима у наредном одељку.
Коришћење NumPy matmul() за множење матрица у Python-у
np.matmul() прима две матрице као улазне параметре и враћа њихов производ ако је множење матрица ваљано.
C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Обратите пажњу на то колико је овај метод једноставнији од претходна два. Уместо np.matmul(), можемо користити еквивалентни оператор @, што ћемо одмах видети.
Како користити оператор @ за множење матрица
У Python-у, @ је бинарни оператор који се користи за множење матрица.
Ради са две матрице, или уопштено, N-димензионалним NumPy низовима и враћа матрицу производа.
Напомена: Оператор @ је доступан у Python-у верзије 3.5 и новијим.
Ево како га користити.
C = [email protected]
print(C)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Запазите да је матрица производа C иста као она коју смо претходно добили.
Да ли се може користити np.dot() за множење матрица?
Ако сте некада наишли на код који користи np.dot() за множење две матрице, ево како то функционише.
C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Видећемо да np.dot(A, B) такође враћа очекивану матрицу производа.
Међутим, према NumPy dokumentaciji, np.dot() треба користити искључиво за израчунавање скаларног производа два једнодимензионална вектора, а не за множење матрица.
Подсетимо се, елемент на позицији (i, j) матрице производа C је скаларни производ i-тог реда матрице A и j-те колоне матрице B.
Пошто NumPy имплицитно примењује ову операцију скаларног производа на све редове и колоне, добијамо резултујућу матрицу производа. Међутим, за читљивији код, уместо np.dot(), требало би да користите np.matmul() или оператор @.
Закључак
🎯 У овом тексту смо научили следеће:
- Услов да би множење матрица било ваљано: број колона матрице A = број редова матрице B.
- Како написати прилагођену Python функцију која проверава да ли је множење матрица ваљано и враћа матрицу производа. Тело функције користи угнежђене
forпетље. - Затим, научили смо како да користимо уграђене листе за множење матрица. Оне су сажетије од
forпетљи, али могу бити мање читљиве. - Коначно, научили смо да користимо NumPy функцију
np.matmul()за множење матрица и зашто је ово најефикаснији приступ. - Такође смо научили о оператору
@за множење две матрице у Python-у.
Тиме завршавамо нашу дискусију о множењу матрица у Python-у. Као следећи корак, можете научити како да проверите да ли је број прост у Python-у или да решавате занимљиве проблеме са Python стринговима.
Срећно учење!🎉