Analiza Big O je metodologija koja se koristi za procenu i kategorizaciju efikasnosti algoritama.
Ona vam omogućava da odaberete algoritme koji su najefikasniji i najbolje se prilagođavaju povećanju obima podataka. Ovaj tekst predstavlja Big O priručnik, objašnjavajući sve ključne aspekte Big O notacije.
Šta je Big O analiza?
Big O analiza je tehnika za procenu kako se algoritmi ponašaju pri povećanju obima podataka. Konkretno, razmatra se koliko efikasan algoritam postaje kako se povećava obim ulaznih podataka.
Efikasnost se odnosi na to koliko se dobro sistemski resursi koriste prilikom generisanja izlaza. Primarni resursi koji su od interesa su vreme i memorija.
Dakle, kada sprovodimo Big O analizu, postavljamo sledeća pitanja:
- Kako se memorijsko opterećenje algoritma menja s povećanjem obima ulaznih podataka?
- Kako se vreme potrebno algoritmu za generisanje izlaza menja s povećanjem obima ulaznih podataka?
Odgovor na prvo pitanje definiše prostornu složenost algoritma, dok odgovor na drugo pitanje definiše njegovu vremensku složenost. Posebna notacija, poznata kao Big O notacija, se koristi za izražavanje odgovora na oba pitanja. Detaljnije ćemo se time baviti u nastavku ovog priručnika.
Preduslovi
Pre nego što nastavimo, neophodno je napomenuti da je za maksimalnu korist od ovog Big O priručnika potrebno osnovno razumevanje algebre. Dodatno, s obzirom da će primeri biti predstavljeni u Python-u, korisno je imati i osnovno znanje o Python-u. Međutim, detaljno znanje nije neophodno jer neće biti potrebno pisati nikakav kod.
Kako sprovesti Big O analizu
U ovom odeljku ćemo se fokusirati na to kako se izvodi Big O analiza.
Prilikom analize složenosti, ključno je imati na umu da performanse algoritma zavise od strukture ulaznih podataka.
Na primer, algoritmi za sortiranje najbrže rade kada su podaci u listi već sortirani u ispravnom redosledu. Ovo predstavlja najbolji slučaj za performanse algoritma. S druge strane, isti algoritmi za sortiranje su najsporiji kada su podaci strukturirani obrnutim redosledom, što predstavlja najgori slučaj.
Prilikom sprovođenja Big O analize, razmatramo isključivo najgori mogući scenario.
Analiza prostorne složenosti

Započnimo ovaj priručnik o Big O analizom načina na koji se analizira prostorna složenost. Želimo da procenimo kako se dodatna memorija koju algoritmi koriste menja sa povećanjem obima ulaznih podataka.
Na primer, funkcija ispod koristi rekurziju za petlju od n do nule. Ona ima prostornu složenost koja je direktno proporcionalna n. To je zato što kako se n povećava, raste i broj poziva funkcije na steku poziva. Dakle, ima složenost prostora od O(n).
def loop_recursively(n):
if n == -1:
return
else:
print(n)
loop_recursively(n - 1)
Međutim, bolja implementacija bi izgledala ovako:
def loop_normally(n):
count = n
while count >= 0:
print(count)
count =- 1
U algoritmu iznad, kreiramo samo jednu dodatnu promenljivu i koristimo je za petlju. Ako bi n raslo sve više i više, i dalje bismo koristili samo jednu dodatnu promenljivu. Dakle, algoritam ima konstantnu prostornu složenost, označenu simbolom „O(1)“.
Upoređujući prostornu složenost dva gorenavedena algoritma, zaključujemo da je `while` petlja efikasnija od rekurzije. To je glavni cilj Big O analize: analizirati kako se algoritmi ponašaju kada se izvršavaju sa većim obimom ulaznih podataka.
Analiza vremenske složenosti

Kada analiziramo vremensku složenost, ne zanima nas porast ukupnog vremena potrebnog algoritmu. Umesto toga, fokusiramo se na rast broja izvršenih računskih koraka. To je zato što stvarno vreme zavisi od brojnih sistemskih i nasumičnih faktora koje je teško objasniti. Stoga, pratimo samo porast računskih koraka i pretpostavljamo da je svaki korak jednak.
Da bismo bolje ilustrovali analizu vremenske složenosti, razmotrimo sledeći primer:
Pretpostavimo da imamo listu korisnika, gde svaki korisnik ima ID i ime. Naš zadatak je da implementiramo funkciju koja vraća ime korisnika kada se unese ID. Evo kako bismo to mogli učiniti:
users = [
{'id': 0, 'name': 'Alice'},
{'id': 1, 'name': 'Bob'},
{'id': 2, 'name': 'Charlie'},
]
def get_username(id, users):
for user in users:
if user['id'] == id:
return user['name']
return 'User not found'
get_username(1, users)
S obzirom na listu korisnika, naš algoritam prolazi kroz celu listu da bi pronašao korisnika sa odgovarajućim ID-om. Kada imamo 3 korisnika, algoritam izvršava 3 iteracije. Kada imamo 10 korisnika, izvršava 10 iteracija.
Dakle, broj koraka je linearno i direktno proporcionalan broju korisnika. Stoga, naš algoritam ima linearnu vremensku složenost. Međutim, možemo poboljšati naš algoritam.
Pretpostavimo da umesto da čuvamo korisnike u listi, čuvamo ih u rečniku. Tada bi naš algoritam za pretragu korisnika izgledao ovako:
users = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def get_username(id, users):
if id in users:
return users[id]
else:
return 'User not found'
get_username(1, users)
Sa ovim novim algoritmom, pretpostavimo da imamo 3 korisnika u našem rečniku; izvršili bismo određeni broj koraka da dobijemo korisničko ime. A pretpostavimo da imamo više korisnika, recimo deset. Izvršili bismo isti broj koraka kao i pre da dobijemo korisnika. Kako broj korisnika raste, broj koraka za dobijanje korisničkog imena ostaje konstantan.
Stoga, ovaj novi algoritam ima konstantnu složenost. Nije važno koliko korisnika imamo; broj izvršenih računskih koraka je isti.
Šta je Big O notacija?
U prethodnom odeljku razgovarali smo o tome kako izračunati prostornu i vremensku složenost Big O za različite algoritme. Koristili smo reči kao što su linearni i konstantan da opišemo složenost. Drugi način da se opiše složenost je upotreba Big O notacije.
Big O notacija je način da se predstavi prostorna ili vremenska složenost algoritma. Zapis je relativno jednostavan; to je O praćeno zagradama. Unutar zagrada pišemo funkciju od n koja predstavlja određenu složenost.
Linearna složenost je predstavljena sa n, pa bismo je zapisali kao O(n) (čita se kao „O od n“). Konstantna složenost je predstavljena sa 1, pa bismo je zapisali kao O(1).
Postoji više složenosti, o kojima ćemo razgovarati u sledećem odeljku. Ali generalno, da biste napisali složenost algoritma, pratite sledeće korake:
- Pokušajte da razvijete matematičku funkciju od n, f(n), gde je f(n) količina iskorišćenog prostora ili računskih koraka koje prati algoritam, a n veličina ulaznih podataka.
- Izaberite najdominantniji termin u toj funkciji. Redosled dominacije različitih termina od najdominantnijeg do najmanje dominantnog je sledeći: faktorijelni, eksponencijalni, polinomski, kvadratni, linearitamski, linearni, logaritamski i konstantni.
- Eliminišite sve koeficijente iz termina.
Rezultat toga postaje termin koji koristimo unutar naših zagrada.
Primer:
Razmotrite sledeću Python funkciju:
users = [
'Alice',
'Bob',
'Charlie'
]
def print_users(users):
number_of_users = len(users)
print("Total number of users:", number_of_users)
for i in number_of_users:
print(i, end=': ')
print(user)
Sada ćemo izračunati vremensku složenost algoritma Big O.
Prvo, pišemo matematičku funkciju od n, f(n), koja predstavlja broj računskih koraka koje algoritam preduzima. Podsetimo se da n predstavlja veličinu ulaznih podataka.
Iz našeg koda, funkcija izvršava dva koraka: jedan za izračunavanje broja korisnika i drugi za štampanje broja korisnika. Zatim, za svakog korisnika izvršava dva koraka: jedan za štampanje indeksa i jedan za štampanje korisnika.
Dakle, funkcija koja najbolje predstavlja broj preduzetih računskih koraka može se napisati kao f(n) = 2 + 2n. Gde je n broj korisnika.
Prelazeći na drugi korak, biramo najdominantniji termin. 2n je linearni član, a 2 je konstantan član. Linearno je dominantnije od konstantnog, pa biramo 2n, linearni član.
Dakle, naša funkcija je sada f(n) = 2n.
Poslednji korak je eliminisanje koeficijenata. U našoj funkciji imamo 2 kao koeficijent. Zato ga eliminišemo. I funkcija postaje f(n) = n. To je termin koji koristimo unutar naših zagrada.
Dakle, vremenska složenost našeg algoritma je O(n) ili linearna složenost.
Različite Big O složenosti
Poslednji odeljak u našem Big O priručniku će vam prikazati različite složenosti i njihove grafikone.
#1. Konstantno

Konstantna složenost znači da algoritam koristi konstantnu količinu prostora (prilikom analize prostorne složenosti) ili konstantan broj koraka (prilikom analize vremenske složenosti). Ovo je najoptimalnija složenost jer algoritmu nije potreban dodatni prostor ili vreme kako ulaz raste. Stoga je veoma skalabilan.
Konstantna složenost je predstavljena kao O(1). Međutim, nije uvek moguće napisati algoritme koji rade u konstantnoj složenosti.
#2. Logaritamski
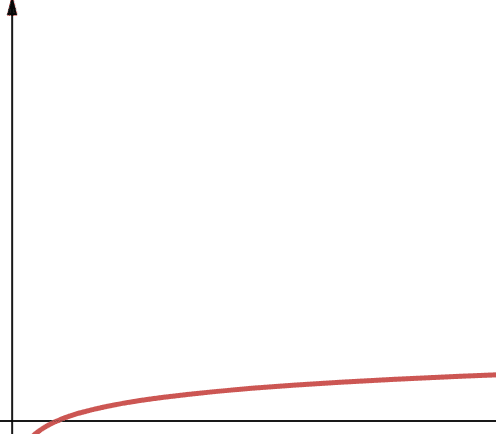
Logaritamska složenost je predstavljena terminom O(log n). Važno je napomenuti da ako baza logaritma nije navedena u računarstvu, pretpostavljamo da je 2.
Prema tome, log n je log2n. Poznato je da logaritamske funkcije u početku brzo rastu, a zatim usporavaju. To znači da se dobro skaliraju i efikasno rade sa sve većim brojem n.
#3. Linearno
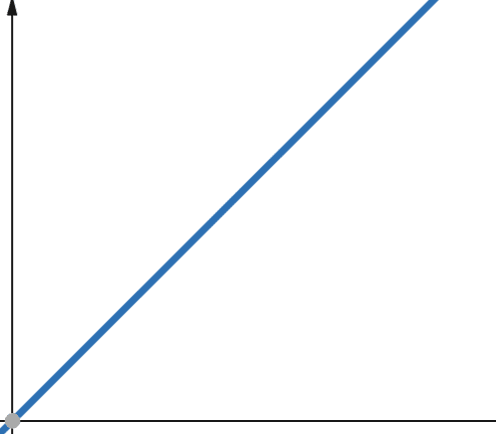
Kod linearnih funkcija, ako se nezavisna promenljiva poveća za faktor p, zavisna promenljiva se povećava za isti faktor p.
Dakle, funkcija sa linearnom složenošću raste za isti faktor kao i veličina ulaznih podataka. Ako se veličina ulaznih podataka udvostruči, povećaće se i broj računskih koraka ili korišćenje memorije. Linearna složenost je predstavljena simbolom O(n).
#4. Linearitamski
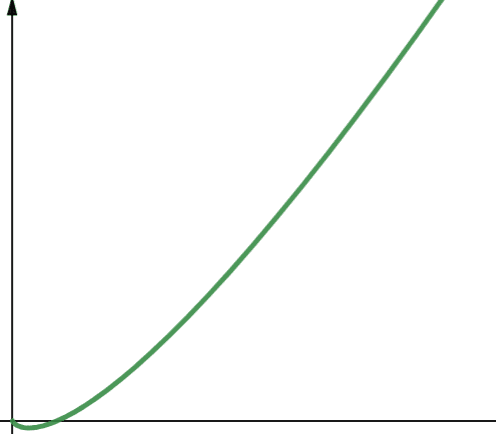
O(n * log n) predstavlja linearitamske funkcije. Linearitamske funkcije su linearna funkcija pomnožena logaritamskom funkcijom. Prema tome, linearitamska funkcija daje rezultate nešto veće od linearnih funkcija kada je log n veće od 1. To je zato što se n povećava kada se pomnoži sa brojem većim od 1.
Log n je veće od 1 za sve vrednosti n veće od 2 (zapamtite, log n je log2n). Stoga, za bilo koju vrednost n veću od 2, linearitamske funkcije su manje skalabilne od linearnih funkcija. Od kojih je n u većini slučajeva veće od 2. Dakle, linearitamske funkcije su generalno manje skalabilne od logaritamskih funkcija.
#5. Kvadratno
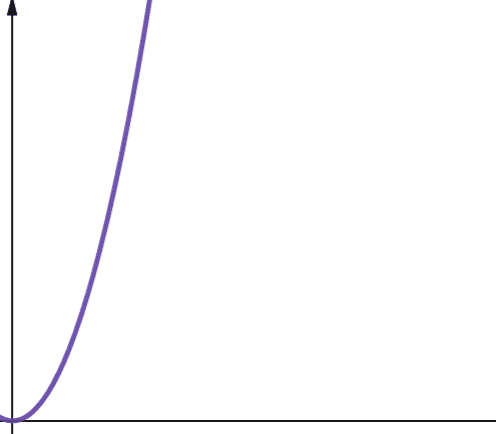
Kvadratna složenost je predstavljena sa O(n2). To znači da ako se veličina vaših ulaznih podataka poveća za 10 puta, broj preduzetih koraka ili iskorišćeni prostor se povećava za 102 puta ili 100! Ovo nije baš skalabilno, i kao što možete videti na grafikonu, složenost se veoma brzo povećava.
Kvadratna složenost nastaje u algoritmima u kojima petljate n puta, i za svaku iteraciju ponovo petljate n puta, na primer, u Bubble Sort algoritmu. Iako generalno nije idealno, ponekad nemate druge opcije osim da implementirate algoritme sa kvadratnom složenošću.
#6. Polinomsko
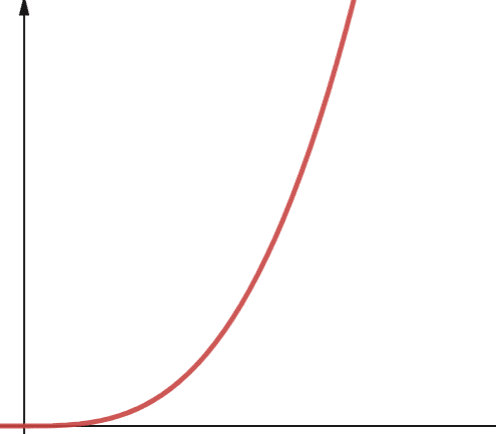
Algoritam sa polinomskom složenošću je predstavljen sa O(np), gde je p neki konstantan ceo broj. P predstavlja red kojim je n podignuto.
Ova složenost nastaje kada imate p broj ugnježdenih petlji. Razlika između polinomske složenosti i kvadratne složenosti je da je kvadratna reda 2, dok polinom ima bilo koji broj veći od 2.
#7. Eksponencijalno
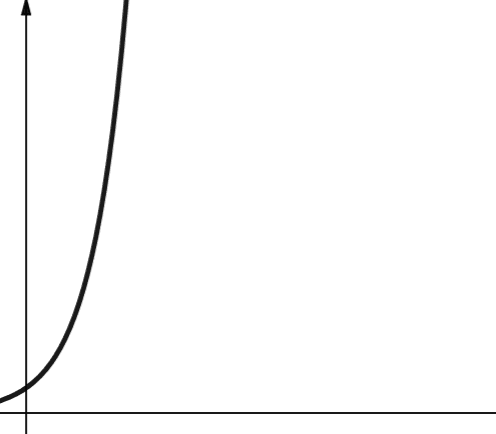
Eksponencijalna složenost raste čak i brže od polinomske složenosti. U matematici, podrazumevana vrednost za eksponencijalnu funkciju je konstanta e (Ojlerov broj). U računarstvu, međutim, podrazumevana vrednost za eksponencijalnu funkciju je 2.
Eksponencijalna složenost je predstavljena simbolom O(2n). Kada je n 0, 2n je 1. Ali kada se n poveća na 5, 2n raste na 32. Povećanje n za jedan će udvostručiti prethodni broj. Prema tome, eksponencijalne funkcije nisu mnogo skalabilne.
#8. Faktorijelno
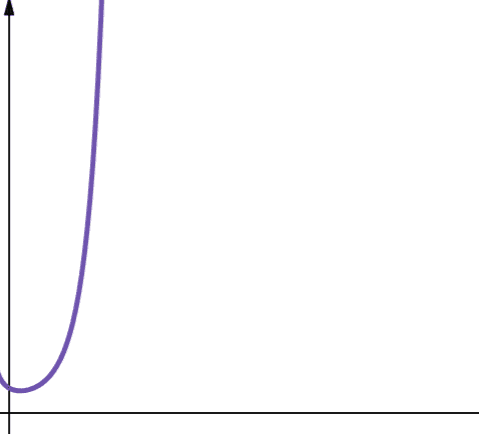
Faktorijelna složenost je predstavljena simbolom O(n!). Ova funkcija takođe raste veoma brzo i stoga nije skalabilna.
Zaključak
Ovaj članak je obradio Big O analizu i kako je izračunati. Takođe smo razgovarali o različitim složenostima i njihovoj skalabilnosti.
Kao sledeći korak, možda biste želeli da vežbate Big O analizu na primeru Python algoritma za sortiranje.