Šta je Testiranje Hipoteza i Kako se Koristi?
Testiranje hipoteza predstavlja ključni metod koji koriste analitičari u različitim sektorima, kako privatnim tako i državnim, kako bi formulisali pouzdane tvrdnje ili pretpostavke zasnovane na podacima o populaciji.
Ako ste se susretali sa analizom podataka o populaciji, verovatno ste već upoznati sa ovom neophodnom alatkom za validaciju pretpostavki.
Postoji mnogo načina za postavljanje pretpostavki, ali nisu svi jednako precizni.
Ukoliko niste sigurni u tačnost svojih podataka, a ipak želite da ih koristite, to može predstavljati rizik za vašu organizaciju.
Testiranje hipoteza je efikasan pristup za postizanje veće preciznosti i igra ključnu ulogu u analizi populacije.
U ovom tekstu, detaljnije ćemo razmotriti šta podrazumeva testiranje hipoteza, kako se primenjuje, koje su njegove prednosti i gde se najčešće koristi.
Započnimo bez daljeg odlaganja!
Definicija Testiranja Hipoteza
Testiranje hipoteza je statistička metoda zaključivanja koju analitičari koriste za procenu da li dostupni podaci o populaciji dovoljno podržavaju određenu hipotezu, kako bi se na osnovu toga donele informisane pretpostavke.
Ova metoda omogućava analitičarima da procene validnost hipoteze i utvrde koliko je pretpostavka tačna, s obzirom na raspoložive podatke.
Jednostavnije rečeno, to je proces testiranja zasnovan na inferencijalnoj statistici, koji omogućava donošenje zaključaka o karakteristikama populacije na osnovu prikupljenih podataka iz uzorka.
Analitičari često ne mogu pristupiti celokupnoj populaciji kako bi utvrdili njene specifične parametre. Međutim, testiranjem hipoteza mogu doneti informisane prognoze i odluke na osnovu podataka iz uzorka i njihove preciznosti.
Vrste Hipoteza u Testiranju
Postoji nekoliko vrsta hipoteza koje se koriste u testiranju:
- Nulta hipoteza: Statistički gledano, pretpostavlja se da podaci iz uzorka nisu značajni i da ne postoji korelacija između dve varijable u okviru posmatranog uzorka.
- Alternativna hipoteza: Ona predstavlja glavnu tezu i suprotstavlja se nultoj hipotezi. U suštini, ona pokreće proces testiranja jer ukazuje na postojanje korelacije između dve varijable u uzorku.
- Neusmerena hipoteza: Predstavlja dvostrano testiranje, gde se pretpostavlja da nema jasnog smera povezanosti između dve varijable u uzorku i da prava vrednost nije ista kao ona koja se predviđa.
- Usmerena hipoteza: Ona opisuje vezu između dve varijable, gde jedna varijabla u uzorku može uticati na drugu.
- Statistička hipoteza: Koristi se za procenu da li podaci i njihova vrednost odgovaraju određenoj hipotezi. Ona je veoma korisna za donošenje zaključaka i pretpostavki o ishodu parametara populacije iz uzorka.
Sada, pogledajmo detaljnije metode koje se koriste u testiranju hipoteza.
Metode Provere Hipoteza
Da bi se utvrdilo da li je neka hipoteza tačna, analitičar treba da ima dovoljno pouzdanih dokaza. U procesu testiranja, nulta i alternativna hipoteza se postavljaju pre same provere.
Testiranje hipoteza ne obuhvata samo jednu metodu, već niz različitih tehnika za procenu podataka iz uzorka. Kao analitičar, neophodno je da uzmete u obzir karakteristike i veličinu uzorka kako biste odabrali odgovarajuću metodu testiranja.
Testiranje Normalnosti
Ova metoda se koristi za analizu regularnosti raspodele podataka u uzorku. Proverava se da li su tačke podataka grupisane oko srednje vrednosti, bilo ispod ili iznad nje.
U statističkom testiranju, šansa da se podaci nalaze iznad ili ispod srednje vrednosti je ista. Formira se zvonasta kriva, koja je simetrična u odnosu na srednju vrednost.
Z-test
Ova metoda se koristi kada su podaci o populaciji normalno raspoređeni. Z-test proverava da li je srednja vrednost dva odvojena parametra populacije različita, kada je poznata varijansa podataka.
Prilikom analize podataka o populaciji, Z-test se često koristi kada je veličina uzorka veća od trideset. Pored toga, Centralna granična teorema, koja tvrdi da sa povećanjem veličine uzorka, uzorci postaju normalno raspoređeni, takođe čini Z-test prikladnom opcijom.
T-test
T-test se koristi kada je veličina uzorka ograničena i podaci su obično raspoređeni. Generalno, T-test se primenjuje kada je veličina uzorka manja od 30, a standardna devijacija populacije nije poznata.
T-test se koristi za izračunavanje intervala poverenja specifičnih podataka o populaciji.
Hi-kvadrat test
Hi-kvadrat test se koristi za procenu prikladnosti i integriteta raspodele podataka.
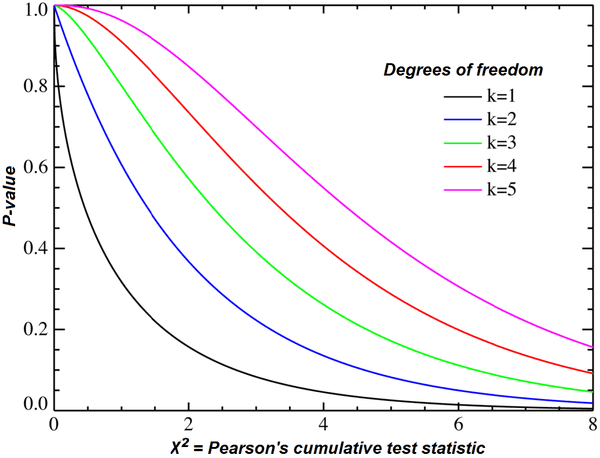
Hi-kvadrat test se često koristi za testiranje varijanse populacije u odnosu na pretpostavljenu ili poznatu vrednost. Postoji nekoliko varijanti Hi-kvadrat testa, ali najčešće se koriste Hi-kvadrat test varijanse i nezavisnosti.
ANOVA Testiranje

ANOVA, ili analiza varijanse, je statistička metoda za poređenje skupova podataka iz dva ili više uzoraka. Omogućava istovremeno poređenje više od dva sredstva.
Takođe, objašnjava zavisnu i nezavisnu varijablu podataka iz uzorka. ANOVA je slična Z-testu i T-testu, ali su potonja dva ograničena na samo dva načina poređenja.
Kako Funkcioniše Testiranje Hipoteza?
Analitičari koriste podatke iz slučajnog uzorka za analizu i merenje. Tokom testiranja, ti podaci se koriste za proveru validnosti nulte i alternativne hipoteze.
Kao što je ranije pomenuto, nulta i alternativna hipoteza se međusobno isključuju, i samo jedna od njih može biti tačna.
Međutim, iako se nulta hipoteza može odbaciti, to ne znači automatski da je alternativna hipoteza uvek tačna.
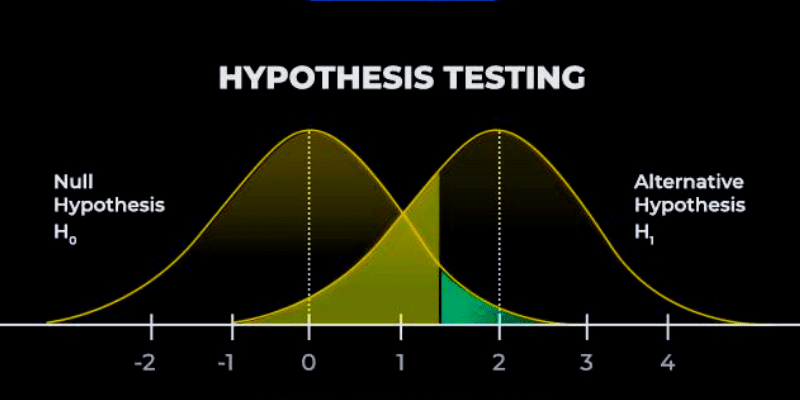
p-vrednost: Tokom procesa testiranja, p-vrednost (verovatnoća) pokazuje da li je rezultat statistički značajan. Takođe, p-vrednost ukazuje na verovatnoću greške prilikom odbacivanja ili prihvatanja nulte hipoteze. Rezultat p-vrednosti je između 0 i 1, i upoređuje se sa nivoom značajnosti.
Nivo značajnosti definiše prihvatljivi rizik od odbacivanja nulte hipoteze. Važno je napomenuti da rezultat testiranja hipoteze može dovesti do dve vrste grešaka:
- Greška tipa 1: Nastaje kada test odbaci nultu hipotezu iako je tačna.
- Greška tipa 2: Nastaje kada test prihvati nultu hipotezu iako je netačna.
Sve vrednosti koje dovode do odbacivanja nulte hipoteze smeštene su u kritičnom regionu. Kritična vrednost je ona koja razdvaja kritični region od ostalih.
Koraci u Testiranju Hipoteza
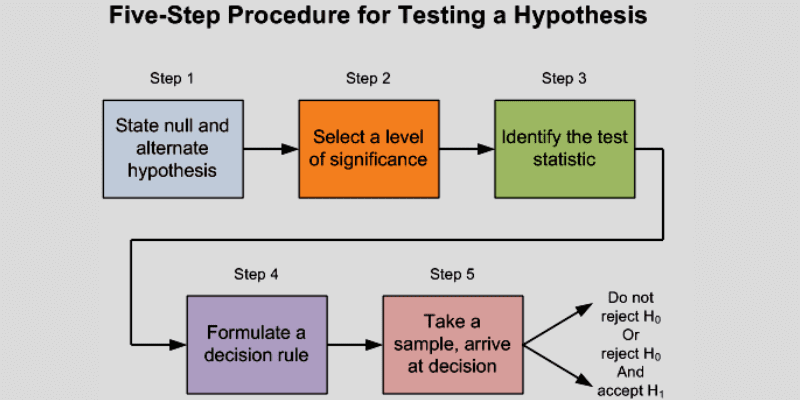
Testiranje hipoteza se generalno sastoji iz četiri koraka:
- Definisanje hipoteza: U prvom koraku, zadatak analitičara je da definiše dve hipoteze, od kojih samo jedna može biti tačna. Nulta hipoteza će ukazati da nema razlike u prosečnom indeksu telesne mase (BMI), dok će alternativna hipoteza tvrditi da postoji značajna razlika.
- Planiranje: U sledećem koraku, neophodno je osmisliti plan analize za obradu podataka iz uzorka. Važno je uzorkovati i prikupiti podatke koji su relevantni za testiranje hipoteze.
- Analiza podataka iz uzorka: Nakon utvrđivanja kako će se podaci procenjivati, sledi analiza podataka iz uzorka, uz proveru da li su uzorci nezavisni i da li su obe veličine uzorka dovoljne.
- Izračunavanje statistike testa: U ovoj fazi, potrebno je izračunati statistiku testa i utvrditi p-vrednost, uz pretpostavku da je nulta hipoteza tačna.
- Procena rezultata: Na kraju, potrebno je proceniti rezultate testiranja hipoteza. Na osnovu podataka iz uzorka, donosi se odluka da li odbaciti nultu hipotezu ili prihvatiti njenu validnost.
U nastavku ćemo razmotriti prednosti testiranja hipoteza.
Prednosti Testiranja Hipoteza
Prednosti testiranja hipoteza su:
- Pomaže u analizi snage tvrdnje zasnovane na podacima.
- Omogućava kreiranje pouzdanog okruženja za donošenje odluka na osnovu uzorka podataka.
- Omogućava utvrđivanje da li su podaci iz uzorka statistički značajni.
- Koristan je za procenu pouzdanosti i validnosti rezultata testa u bilo kom sistematičnom procesu testiranja.
Takođe, pomaže u ekstrapolaciji podataka iz faze uzorka na veću populaciju, u zavisnosti od potreba.
Primeri Upotrebe Testiranja Hipoteza
Testiranje hipoteza koristi se u različitim sektorima kako bi se procenila tačnost podataka iz uzorka. Neki od primera su:
#1. Klinička ispitivanja
Testiranje hipoteza se često koristi u kliničkim ispitivanjima kako bi se utvrdilo da li je novi lek, tretman ili procedura efikasna, na osnovu podataka iz uzorka.
Na primer, lekar može pretpostaviti da određeni tretman može sniziti nivo kalijuma kod pacijenata. On će izmeriti nivo kalijuma kod grupe pacijenata pre tretmana i ponovo nakon tretmana.

Zatim, lekar sprovodi testiranje hipoteze, gde je H0: Uposle = Upre, što znači da je nivo kalijuma isti nakon tretmana kao i pre njega. Alternativna hipoteza je Ha: Uposle < Upre, što znači da je nivo kalijuma smanjen nakon primene tretmana.
Ako je p-vrednost manja od nivoa značajnosti, lekar može zaključiti da je tretman efikasan u snižavanju nivoa kalijuma.
#2. Proizvodnja
Testiranje hipoteza se koristi u proizvodnim pogonima kako bi se utvrdilo da li je nova metoda ili tehnika efikasna.
Na primer, kompanija može koristiti testiranje hipoteza da bi utvrdila da li nova metoda smanjuje broj neispravnih proizvoda po seriji. Pretpostavimo da je prosečan broj neispravnih proizvoda 300 po seriji.

Proizvođač treba da utvrdi prosečan broj neispravnih proizvoda pre i posle uvođenja nove metode. Oni mogu testirati hipoteze H0: Uposle = Upre, što znači da je prosečan broj neispravnih proizvoda isti kao i pre uvođenja metode.
Alternativna hipoteza je HA: Uposle nije jednako Upre, što znači da je ukupan broj neispravnih proizvoda promenjen nakon uvođenja nove metode.
Ako je p-vrednost manja od nivoa značajnosti, kompanija može zaključiti da se broj neispravnih proizvoda promenio.
#3. Poljoprivreda
Testiranje hipoteza se često koristi u poljoprivredi kako bi se utvrdilo da li određeno đubrivo ili pesticid utiče na rast i imunitet biljaka. Biolozi mogu testirati da li će određena biljka porasti više od 15 inča nakon primene novog đubriva.

Biolog primenjuje đubrivo mesec dana kako bi prikupio podatke o uzorcima. Jedna od hipoteza bi bila H0 U=15 inča, što ukazuje da đubrivo ne poboljšava prosečan rast biljke.
Alternativna hipoteza je HA: U> 15 inča, što znači da đubrivo povećava prosečan rast biljke. Nakon testiranja, ako je p-vrednost manja od nivoa značajnosti, biolog može dokazati da đubrivo uzrokuje veći rast biljke.
Resursi za Učenje
#1. Statistika: Udemy korak po korak uvod

Udemy nudi kurs o statistici koji vas vodi kroz korak po korak uvod, uključujući testiranje hipoteza. Kurs obuhvata primere i lekcije bivšeg Google-ovog data scientist-a koji će vam pomoći da ovladate intervalima poverenja, testovima hipoteza i drugim temama.
#2. Osnovna statistika za analizu podataka od strane Udemy
Ovaj Udemy kurs o osnovnoj statistici za analizu podataka pomoći će vam da savladate statistiku kroz projekte iz stvarnog sveta, testove hipoteza, distribucije verovatnoće, regresionu analizu i mnoge druge teme.
#3. Statistika za nauku o podacima i poslovnu analizu

Ovaj Udemy kurs o statistici za nauku o podacima i poslovnu analizu pomoći će vam da naučite testiranje hipoteza. Kurs pokriva različite statističke teme, omogućavajući data scientist-ima i poslovnim analitičarima da ih savladaju. Obuhvata inferencijalnu i deskriptivnu statistiku, kao i regresionu analizu.
#4. Testiranje hipoteza Džima Frosta
Ova knjiga, dostupna na Amazonu, predstavlja intuitivni vodič koji pomaže analitičarima da donose odluke zasnovane na podacima.
Objašnjava kako funkcionišu testovi hipoteza, zašto su vam potrebni, kako koristiti intervale poverenja, p-vrednosti, nivoe značajnosti i mnoge druge teme.
#5. Testiranje hipoteza Skota Hartshorna
Ova knjiga se izdvaja po vizuelnim primerima i predstavlja najbolji izbor za početnike koji traže brz vodič za testiranje hipoteza.
Upoznaje vas sa značajem statistike, različitim vrstama testova i njihovim funkcionisanjem. Nije potrebno imati detaljno prethodno znanje iz statistike, jer su sve teme objašnjene na intuitivan način.
Završna Reč
Testiranje hipoteza pomaže u validaciji pretpostavki, a zatim u razvoju statističkih zaključaka na osnovu procena. Koristi se u mnogim sektorima, od proizvodnje i poljoprivrede, do kliničkih ispitivanja i IT-a. Ovaj metod je ne samo precizan, već vam pomaže i da donosite odluke zasnovane na podacima za vašu organizaciju.
Za dalje usavršavanje, pogledajte preporučene resurse za učenje kako biste postali stručni poslovni analitičar.